
【題目】設![]() ,函數
,函數![]() .
.
(1)若![]() ,求
,求![]() 的反函數
的反函數![]() ;
;
(2)求函數![]() 的最大值(用
的最大值(用![]() 表示);
表示);
(3)設![]() ,若對任意
,若對任意![]() ,
,![]() 恒成立,求
恒成立,求![]() 的范圍.
的范圍.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)根據反函數定義求解即可;
(2)根據y=f(x)f(﹣x),判斷函數y的單調性即可求解最大值.
(3)g(x)=f(x)﹣f(x﹣1)![]() ,換元t=a2x,得h(t)
,換元t=a2x,得h(t)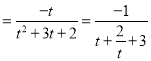 ,討論
,討論![]() 和
和![]() 時,h(t)最值即可求解
時,h(t)最值即可求解
(1)當a=1時,f(x)![]() ,
,
∴1+2x![]() ,
,
即2x![]() 1
1![]() ,則0<y<1,
,則0<y<1,
∴x=log2(![]() );
);
故f(x)的反函數f﹣1(x)=log2(![]() ),x∈(0,1)
),x∈(0,1)
(2)∵y=f(x)f(﹣x)![]()
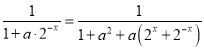 ,
,
設y=2x+2﹣x,易知,函數y=2x+2﹣x在(﹣∞,0)上單調遞減,在(0,+∞)上單調遞增,
則當x=0時,y=2x+2﹣x有最小值,最小值為2,
∴當x=0時,y=f(x)f(﹣x)有最大值,
∴ymax![]() ;
;
(3)g(x)=f(x)﹣f(x﹣1)![]() ,令t=a2x,∵x∈(﹣∞,0],a>0,∴0<t≤a.
,令t=a2x,∵x∈(﹣∞,0],a>0,∴0<t≤a.
∴h(t)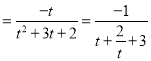 ,
,
當![]() 時h(t)在(0,a]上單調遞減,所以
時h(t)在(0,a]上單調遞減,所以![]()
∵對任意x∈(﹣∞,0],g(x)≥g(0)恒成立,且g(0) ,
,
∴ 恒成立,∴0
恒成立,∴0![]()
當![]() 時,
時, ,令
,令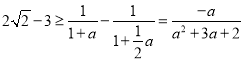 不恒成立,舍去
不恒成立,舍去
綜上,a的取值范圍是(0,![]() ].
].


 王后雄學案教材完全解讀系列答案
王后雄學案教材完全解讀系列答案 海淀課時新作業金榜卷系列答案
海淀課時新作業金榜卷系列答案科目:高中數學 來源: 題型:
【題目】已知集合M是滿足下列性質的函數![]() 的全體;在定義域內存在實數t,使得
的全體;在定義域內存在實數t,使得![]() .
.
(1)判斷![]() 是否屬于集合M,并說明理由;
是否屬于集合M,并說明理由;
(2)若![]() 屬于集合M,求實數a的取值范圍;
屬于集合M,求實數a的取值范圍;
(3)若![]() ,求證:對任意實數b,都有
,求證:對任意實數b,都有![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
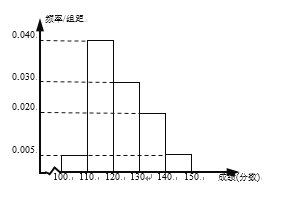
【題目】遼寧省六校協作體(葫蘆島第一高中、東港二中、鳳城一中、北鎮高中、瓦房店高中、丹東四中)中的某校理科實驗班的100名學生期中考試的語文、數學成績都不低于100分,其中語文成績的頻率分布直方圖如圖所示,成績分組區間是:[100,110),[110,120),[120,130),[130,140),[140,150].
這100名學生語文成績某些分數段的人數![]() 與數學成績相應分數段的人數
與數學成績相應分數段的人數![]() 之比如下表所示:
之比如下表所示:
分組區間 | [100,110) | [110,120) | [120,130) | [130,140) |
| 1:2 | 2:1 | 3:4 | 1:1 |
(1)估計這100名學生語文成績的平均數、方差(同一組數據用該區間的中點值作代表);
(2)從數學成績在[130,150] 的學生中隨機選取2人,該2人中數學成績在[140,150]的人數為![]() ,求
,求![]() 的數學期望
的數學期望![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列四個命題中真命題是![]()
![]()
A. 同垂直于一直線的兩條直線互相平行
B. 底面各邊相等,側面都是矩形的四棱柱是正四棱柱
C. 過空間任一點與兩條異面直線都垂直的直線有且只有一條
D. 過球面上任意兩點的大圓有且只有一個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 都是由實數組成的無窮數列.
都是由實數組成的無窮數列.
(1)若![]() 都是等差數列,判斷數列
都是等差數列,判斷數列![]() 是否是等差數列,說明理由;
是否是等差數列,說明理由;
(2)若![]() ,且
,且![]() 是等比數列,求
是等比數列,求![]() 的所有可能值;
的所有可能值;
(3)若![]() 都是等差數列,數列
都是等差數列,數列![]() 滿足
滿足![]() ,求證:
,求證: ![]() 是等差數列的充要條件是:
是等差數列的充要條件是: ![]() 中至少有一個是常數.
中至少有一個是常數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com