
分析 (1)由題意可得第4月的保有量為Q=(a1-b1)+(a2-b2)+(a3-b3)+(a4-b4),代入計算即可得到所求值;
(2)計算當n≥4時,Q=935+(-10×5+470)-(5+5)+…+(-10n+470)-(n+5),應用等差數列的求和公式,化簡整理可得Q,再由二次函數的性質,可得Q的最大值,求出此時自行車停放點容納車輛,比較即可得到結論.
解答 解:(1)an=$\left\{\begin{array}{l}{5{n}^{4}+15,n∈[1,3]}\\{-10n+470,n∈[4,+∞)}\end{array}\right.$,n∈N*,bn=n+5(n∈N*),
可得第4月的保有量為Q=(a1-b1)+(a2-b2)+(a3-b3)+(a4-b4)
=(5+15-6)+(5×16+15-7)+(5×81+15-8)+(-40+470-9)=14+88+412+421=935;
(2)當n≥4時,Q=935+(-10×5+470)-(5+5)+…+(-10n+470)-(n+5)
=935+(-10)×$\frac{(n-4)(n+5)}{2}$+470(n-4)-$\frac{(n-4)(n+5)}{2}$-5(n-4)
=-$\frac{11}{2}$n2+$\frac{919}{2}$n-815,
可得Q=$\left\{\begin{array}{l}{14,n=1}\\{102,n=2}\\{514,n=3}\\{-\frac{11}{2}{n}^{2}+\frac{919}{2}n-815,n≥4}\end{array}\right.$,n∈N*,
n≥4時,由于對稱軸為-$\frac{919}{2×11}$與42距離最小,
則當n=42時,Q取得最大值8782.
此時,S42=-(42-46)2+8800=8784>8782.
則當Q取最大值時,停放點能容納.
點評 本題考查函數模型在實際問題中的應用,考查二次函數的最值求法,注意n為自然數,考查化簡整理的運算能力,屬于中檔題.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
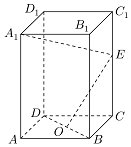 如圖,正四棱柱ABCD-A1B1C1D1中,O是BD的中點,E是棱CC1上任意一點.
如圖,正四棱柱ABCD-A1B1C1D1中,O是BD的中點,E是棱CC1上任意一點.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 圓 | B. | 橢圓 | C. | 雙曲線 | D. | 直線 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
 如圖,ABCD是邊長為$2\sqrt{3}$的正方形,點E,F分別是邊BC,CD的中點,將△ABE,△CEF,△ADF分別沿AE,EF,FA折起,使得B,C,D三點重合于點P,若四面體PAEF的四個頂點在同一個球的球面上,則該球的表面積是( )
如圖,ABCD是邊長為$2\sqrt{3}$的正方形,點E,F分別是邊BC,CD的中點,將△ABE,△CEF,△ADF分別沿AE,EF,FA折起,使得B,C,D三點重合于點P,若四面體PAEF的四個頂點在同一個球的球面上,則該球的表面積是( )| A. | 6π | B. | 12π | C. | 18π | D. | $9\sqrt{2}π$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com