
分析 解方程fm(x)=fn(x)得交點P($\frac{m+n-1}{2}$,$(\frac{n-m-1}{2})^{2}-m$),函數f(x)的圖象與直線l:y=-x+n-m有四個不同的交點,由圖象知,點P在l的上方,故$\frac{m+n-1}{2}+(\frac{n-m-1}{2})^{2}-m-(n-m)$>0,由此解得m-n的取值范圍.
解答 解:作函數f(x)的圖象,解方程fm(x)=fn(x),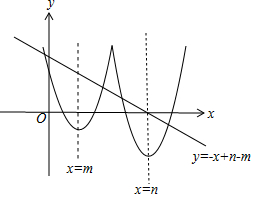
得x=$\frac{m+n-1}{2}$,即交點P($\frac{m+n-1}{2}$,$(\frac{n-m-1}{2})^{2}-m$),
又函數y=f(x)+x+m-n有四個零點,
即函數f(x)的圖象與直線l:y=-x+n-m有四個不同的交點.
由圖象知,點P在l的上方,
∴$\frac{m+n-1}{2}+(\frac{n-m-1}{2})^{2}-m-(n-m)$>0,
即(n-m)2-4(n-m)-1>0,
解得:n-m$<2-\sqrt{5}$或n-m$>2+\sqrt{5}$.
∵m<n,∴n-m>$2+\sqrt{5}$,
即m-n<-($2+\sqrt{5}$).
故答案為:(-∞,-2-$\sqrt{5}$).
點評 本題主要考查根的存在性以及根的個數判斷,函數的零點與方程的根的關系,體現了轉化的數學思想,屬于中檔題.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:選擇題
| A. | y平均減少2.5個單位 | B. | y平均減少0.5個單位 | ||
| C. | y平均增加2.5個單位 | D. | y平均增加0.5個單位 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 一個命題的逆命題為真,則它的逆否命題一定為真 | |
| B. | 若“ac2>bc2”,則a>b | |
| C. | ?x0∈R,$sin{x_0}+cos{x_0}=\frac{3}{2}$ | |
| D. | “a2+b2=0,則a,b全為0”的逆否命題是“若a,b全不為0,則a2+b2≠0” |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | 0 | C. | -i | D. | i |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 15 | B. | 30 | C. | 45 | D. | 60 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
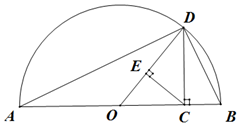 若a>0,b>0,則稱$\frac{2ab}{a+b}$為a,b的調和平均數.如圖,點C為線段AB上的點,且AC=a,BC=b,點O為線段AB中點,以AB為直徑做半圓,過點C作AB的垂線交半圓于D,連結OD,AD,BD.過點C作OD的垂線,垂足為E,則圖中線段OD的長度是a,b的算術平均數,那么圖中表示a,b的幾何平均數與調和平均數的線段,以及由此得到的不等關系分別是( )
若a>0,b>0,則稱$\frac{2ab}{a+b}$為a,b的調和平均數.如圖,點C為線段AB上的點,且AC=a,BC=b,點O為線段AB中點,以AB為直徑做半圓,過點C作AB的垂線交半圓于D,連結OD,AD,BD.過點C作OD的垂線,垂足為E,則圖中線段OD的長度是a,b的算術平均數,那么圖中表示a,b的幾何平均數與調和平均數的線段,以及由此得到的不等關系分別是( )| A. | $CD,CE,\frac{2ab}{a+b}≥\sqrt{ab}$ | B. | $CD,DE,\frac{2ab}{a+b}≤\sqrt{ab}$ | C. | $CD,CE,\frac{2ab}{a+b}≥\sqrt{ab}$ | D. | $CD,CE,\frac{2ab}{a+b}≤\sqrt{ab}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com