【題目】如圖，在三棱錐
中，
，
，
為
的中點．
（1）證明：
平面
；
（2）若點
在棱
上，且二面角
為
，求
與平面
所成角的正弦值．
【答案】（1）見解析（2）
【解析】分析：(1)根據等腰三角形性質得PO垂直AC，再通過計算，根據勾股定理得PO垂直OB，最后根據線面垂直判定定理得結論，(2)根據條件建立空間直角坐標系，設立各點坐標，根據方程組解出平面PAM一個法向量，利用向量數量積求出兩個法向量夾角，根據二面角與法向量夾角相等或互補關系列方程，解得M坐標，再利用向量數量積求得向量PC與平面PAM法向量夾角，最后根據線面角與向量夾角互余得結果.
詳解：（1）因為
，
為
的中點，所以
，且
.
連結
.因為
，所以
為等腰直角三角形，
且
，
.
由
知
.
由
知
平面
.
（2）如圖，以為坐標原點，
的方向為
軸正方向，建立空間直角坐標系
.
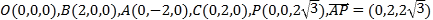
由已知得
取平面
的法向量
.
設
，則
.
設平面
的法向量為
.
由
得
，可取
，
所以
.由已知得
.
所以
.解得
（舍去），
.
所以
.又
，所以
.
所以
與平面所成角的正弦值為.
七星圖書口算速算天天練系列答案科目：高中數學 來源： 題型：
【題目】袋子中有四個小球，分別寫有“文、明、中、國”四個字，有放回地從中任取一個小球，直到“中”“國”兩個字都取到就停止，用隨機模擬的方法估計恰好在第三次停止的概率．利用電腦隨機產生0到3之間取整數值的隨機數，分別用0，1，2，3代表“文、明、中、國”這四個字，以每三個隨機數為一組，表示取球三次的結果，經隨機模擬產生了以下18組隨機數：
232 321 230 023 123 021 132 220 001
231 130 133 231 013 320 122 103 233
由此可以估計，恰好第三次就停止的概率為( )
A.
B.
C.
D.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】有
名學生排成一排，求分別滿足下列條件的排法種數，要求列式并給出計算結果.
（1）甲不在兩端；
（2）甲、乙相鄰；
（3）甲、乙、丙三人兩兩不得相鄰；
（4）甲不在排頭，乙不在排尾。
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知
、
是橢圓
：
的左右焦點，焦距為6，橢圓上存在點
使得
，且
的面積為9.
（Ⅰ）求的方程；
（Ⅱ）過的直線
與橢圓相交于
，
兩點，直線與
軸不重合，
是
軸上一點，且
，求點縱坐標的取值集合.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
，設直線
分別是曲線
的兩條不同的切線；
（1）若函數
為奇函數，且當
時，有極小值為-4；
（i）求
的值；
（ii）若直線
亦與曲線相切，且三條不同的直線
交于點
，求實數m的取值范圍；
（2）若直線
，直線
與曲線切于點B且交曲線于點D，直線
與曲線切于點C且交曲線于點A，記點
的橫坐標分別為
，求
的值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知點
是函數
的圖象上的一點，等比數列
的前
項和為
，數列
的首項為
，且前項和
滿足：
.
（1）求數列，的通項公式；
（2）若數列
的通項
，求數列的前項和
；
（3）若數列
的前項和為
，是否存在最大的整數
，使得對任意的正整數n，均有
總成立？若成立，求出t；若不存在，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知某種細菌的適宜生長溫度為
，為了研究該種細菌的繁殖數量
（單位：個）隨溫度
（單位：
）變化的規律，收集數據如下：
溫度 | 12 | 14 | 16 | 18 | 20 | 22 | 24 |
繁殖數量 | 20 | 25 | 33 | 27 | 51 | 112 | 194 |
對數據進行初步處理后，得到了一些統計量的值，如下表所示：
|
|
|
|
|
|
|
18 | 66 | 3.8 | 112 | 4.3 | 1428 | 20.5 |
其中
，
.
（1）請繪出關于的散點圖，并根據散點圖判斷
與
哪一個更適合作為該種細菌的繁殖數量關于的回歸方程類型（結果精確到0.1）；
（2）當溫度為
時，該種細菌的繁殖數量的預報值為多少？
參考公式：對于一組數據
，其回歸線
的斜率和截距的最小二乘估計分別為：
，
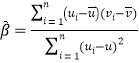.參考數據：
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
