
分析 由曲線C的方程可得x2+y2≥1,|x|≤1,|y|≤1,從而可得出曲線C的大體范圍,結合圖形推導結論.
解答 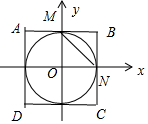 解:設P(x,y)是曲線上一點,則P關于x軸的對稱點(x,-y)顯然也在曲線C上,
解:設P(x,y)是曲線上一點,則P關于x軸的對稱點(x,-y)顯然也在曲線C上,
∴曲線C關于x軸對稱,
同理可得曲線C關于y軸對稱,關于原點對稱,故①正確;
∵x2=1-y4=(1-y2)•(1+y2)≥(1-y2),∴x2+y2≥1,即$\sqrt{{x}^{2}+{y}^{2}}$≥1.
∴曲線上任意一點到原點的距離最小值為1,(當且僅當y=0時,x等于1)
故②錯誤;
由②可得,曲線C所上的點在單位圓x2+y2=1的外部或圓上,∴S>π,
由x2+y4=1可得|x|≤1,|y|≤1,(不能同時取1)
∴曲線C上的點在以2為邊長的正方形ABCD內部或邊上,∴S<4,
故④正確;
設曲線C的上頂點為M,右頂點為N,則MN=$\sqrt{2}$,
由兩點之間線段最短可知曲線C在第一象限內的長度大于$\sqrt{2}$,
同理曲線C在每一象限內的長都大于$\sqrt{2}$,故l>4$\sqrt{2}$,故③正確.
故答案為:3.
點評 本題考查曲線的性質,命題的真假判斷,注意運用不等式的性質和數形結合的思想方法,考查推理能力和判斷能力,屬于中檔題.


 輕松奪冠全能掌控卷系列答案
輕松奪冠全能掌控卷系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{2π}{3}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{3}{2}$-$\frac{\sqrt{3}}{2}$i | B. | $\frac{3}{4}$-$\frac{\sqrt{3}}{4}$i | C. | $\frac{3}{2}$+$\frac{\sqrt{3}}{2}$i | D. | $\frac{3}{4}$+$\frac{\sqrt{3}}{4}$i |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
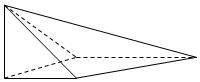 如圖,在四棱錐S-ABCD中,SA⊥平面ABCD,底面ABCD為直角梯形,AD∥BC,∠ABC=90°,SA=AB=AD=1,BC=2.
如圖,在四棱錐S-ABCD中,SA⊥平面ABCD,底面ABCD為直角梯形,AD∥BC,∠ABC=90°,SA=AB=AD=1,BC=2.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com