
【題目】某地1~10歲男童年齡![]() (單位:歲)與身高的中位數
(單位:歲)與身高的中位數![]() (單位
(單位![]() ,如表所示:
,如表所示:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 76.5 | 88.5 | 96.8 | 104.1 | 111.3 | 117.7 | 124 | 130 | 135.4 | 140.2 |
對上表的數據作初步處理,得到下面的散點圖及一些統計量的值.
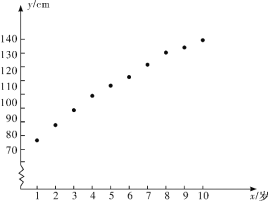
|
|
|
|
112.45 | 82.50 | 3947.71 | 566.85 |
(1)求![]() 關于
關于![]() 的線性回歸方程(回歸方程系數精確到0.01);
的線性回歸方程(回歸方程系數精確到0.01);
(2)某同學認為方程![]() 更適合作為
更適合作為![]() 關于
關于![]() 的回歸方程模型,他求得的回歸方程是
的回歸方程模型,他求得的回歸方程是![]() .經調查,該地11歲男童身高的中位數為
.經調查,該地11歲男童身高的中位數為![]() ,與(1)中的線性回歸方程比較,哪個回歸方程的擬合效果更好?
,與(1)中的線性回歸方程比較,哪個回歸方程的擬合效果更好?
(3)從6歲~10歲男童中每個年齡階段各挑選一位男童參加表演(假設該年齡段身高的中位數就是該男童的身高).再從這5位男童中任挑選兩人表演“二重唱”,則“二重唱”男童身高滿足![]() 的概率是多少?
的概率是多少?
參考公式: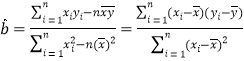 ,
,![]()
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,直線
中,直線![]() 與原點
與原點![]() 為圓心的圓相交所得弦長為
為圓心的圓相交所得弦長為![]() .
.
(1)若直線![]() 與圓
與圓![]() 切于第一象限,且直線
切于第一象限,且直線![]() 與坐標軸交于點
與坐標軸交于點![]() ,當
,當![]() 面積最小時,求直線
面積最小時,求直線![]() 的方程;
的方程;
(2)設![]() 是圓
是圓![]() 上任意兩點,點
上任意兩點,點![]() 關于
關于![]() 軸的對稱點為
軸的對稱點為![]() ,若直線
,若直線![]() 分別交于
分別交于![]() 軸與點
軸與點![]() 和
和![]() ,問
,問![]() 是否為定值?若是,請求處該定值;若不是,請說明理由.
是否為定值?若是,請求處該定值;若不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近日,某地普降暴雨,當地一大型提壩發生了滲水現象,當發現時已有![]() 的壩面滲水,經測算,壩而每平方米發生滲水現象的直接經濟損失約為
的壩面滲水,經測算,壩而每平方米發生滲水現象的直接經濟損失約為![]() 元,且滲水面積以每天
元,且滲水面積以每天![]() 的速度擴散.當地有關部門在發現的同時立即組織人員搶修滲水壩面,假定每位搶修人員平均每天可搶修滲水面積
的速度擴散.當地有關部門在發現的同時立即組織人員搶修滲水壩面,假定每位搶修人員平均每天可搶修滲水面積![]() ,該部門需支出服裝補貼費為每人
,該部門需支出服裝補貼費為每人![]() 元,勞務費及耗材費為每人每天
元,勞務費及耗材費為每人每天![]() 元.若安排
元.若安排![]() 名人員參與搶修,需要
名人員參與搶修,需要![]() 天完成搶修工作.
天完成搶修工作.
![]() 寫出
寫出![]() 關于
關于![]() 的函數關系式;
的函數關系式;
![]() 應安排多少名人員參與搶修,才能使總損失最小.(總損失=因滲水造成的直接損失+部門的各項支出費用)
應安排多少名人員參與搶修,才能使總損失最小.(總損失=因滲水造成的直接損失+部門的各項支出費用)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P—ABCD中,四邊形ABCD是矩形,平面PCD⊥平面ABCD,M為PC中點.求證:
(1)PA∥平面MDB;
(2)PD⊥BC.
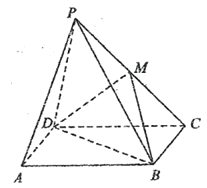
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com