
| A. | $\sqrt{2}$ | B. | $\frac{-3+6\sqrt{2}}{4}$ | C. | $\sqrt{3}$ | D. | $\frac{3+6\sqrt{2}}{7}$ |
分析 設F1N=ON=MN=r,則OF2=2r,根據勾股定理NF2=2$\sqrt{2}$r,再利用相似三角形和雙曲線的離心率公式即可求得
解答 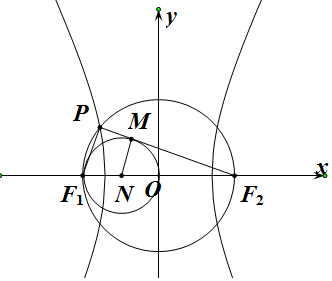 解:設F1N=ON=MN=r,
解:設F1N=ON=MN=r,
則OF2=2r,
根據勾股定理NF2=2$\sqrt{2}$r,
又△MF2N∽△PF1F2,
∴e=$\frac{c}{a}$=$\frac{2c}{2a}$=$\frac{{F}_{1}{F}_{2}}{P{F}_{2}-P{F}_{1}}$=$\frac{N{F}_{2}}{M{F}_{2}-MN}$=$\frac{3r}{2\sqrt{2}r-r}$=$\frac{6\sqrt{2}+3}{7}$,
故選:D
點評 此題要求學生掌握定義:到兩個定點的距離之差等于|2a|的點所組成的圖形即為雙曲線.考查了數形結合思想、本題凸顯解析幾何的特點:“數研究形,形助數”,利用幾何性質可尋求到簡化問題的捷徑.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | {0,2,3} | B. | {-2,1,2,3} | C. | {-1,0,2,3} | D. | {2,3} |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
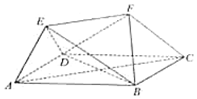 如圖,在多面體ABCDEF中,底面ABCD是菱形,AB=2,∠DAB=60°,EF∥AC,EF=$\sqrt{3}$.
如圖,在多面體ABCDEF中,底面ABCD是菱形,AB=2,∠DAB=60°,EF∥AC,EF=$\sqrt{3}$.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 6 | B. | 8 | C. | 9 | D. | 10 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題

| A. | x≥0? | B. | x≥1? | C. | x≥-1? | D. | x≥-3? |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| 特征量 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次 |
| x | 555 | 559 | 551 | 563 | 552 |
| y | 601 | 605 | 597 | 599 | 598 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com