
【題目】已知函數(shù)![]() ,
,![]() .
.
(1)若![]() ,判斷函數(shù)
,判斷函數(shù)![]() 的單調(diào)性并說明理由;
的單調(diào)性并說明理由;
(2)若![]() ,求證:關(guān)
,求證:關(guān)![]() 的不等式
的不等式![]() 在
在![]() 上恒成立.
上恒成立.
【答案】(1)函數(shù)![]() 在
在![]() 上單調(diào)遞減,理由見解析;(2)證明見解析.
上單調(diào)遞減,理由見解析;(2)證明見解析.
【解析】
(1)求出函數(shù)![]() 的導數(shù),分析導數(shù)
的導數(shù),分析導數(shù)![]() 在區(qū)間
在區(qū)間![]() 上的符號,即可得出結(jié)論;
上的符號,即可得出結(jié)論;
(2)將所證不等式變形為![]() ,證明出
,證明出![]() ,于是將不等式轉(zhuǎn)化為證明
,于是將不等式轉(zhuǎn)化為證明![]() ,通過證明出
,通過證明出![]() ,將不等式轉(zhuǎn)化為
,將不等式轉(zhuǎn)化為![]() ,然后構(gòu)造函數(shù)
,然后構(gòu)造函數(shù)![]() ,利用單調(diào)性證明即可.
,利用單調(diào)性證明即可.
(1)函數(shù)![]() 在
在![]() 上單調(diào)遞減,理由如下:
上單調(diào)遞減,理由如下:
依題意![]() ,
,![]() ,則
,則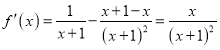 .
.
當![]() 時,
時,![]() ,故函數(shù)
,故函數(shù)![]() 在
在![]() 上單調(diào)遞減;
上單調(diào)遞減;
(2)要證![]() ,即證
,即證![]() ,
,
即證![]() .
.
設![]() ,則
,則![]() .
.
當![]() 時,
時,![]() ,所以
,所以![]() 在
在![]() 上單調(diào)遞增,
上單調(diào)遞增,
所以![]() ,即
,即![]() .
.
故當![]() 時,
時,![]() ,
,
故即證![]() .
.
令![]() ,
,![]() .
.
由(1)可知,![]() ,
,
故![]() 在
在![]() 上單調(diào)遞增.
上單調(diào)遞增.
所以,當![]() 時,
時,![]() ,即
,即![]() ,
,
所以,當![]() 時,
時,![]() ,
,
所以只需證明![]() ,即證明
,即證明![]() .
.
設![]() ,則
,則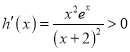 .
.
所以![]() 在
在![]() 上單調(diào)遞增,所以
上單調(diào)遞增,所以![]() ,所以原不等式成立.
,所以原不等式成立.


科目:高中數(shù)學 來源: 題型:
【題目】(多選題)下列說法中,正確的命題是( )
A.已知隨機變量![]() 服從正態(tài)分布
服從正態(tài)分布![]() ,
,![]() ,則
,則![]() .
.
B.以模型![]() 去擬合一組數(shù)據(jù)時,為了求出回歸方程,設
去擬合一組數(shù)據(jù)時,為了求出回歸方程,設![]() ,將其變換后得到線性方程
,將其變換后得到線性方程![]() ,則
,則![]() ,
,![]() 的值分別是
的值分別是![]() 和0.3.
和0.3.
C.已知兩個變量具有線性相關(guān)關(guān)系,其回歸直線方程為![]() ,若
,若![]() ,
,![]() ,
,![]() ,則
,則![]() .
.
D.若樣本數(shù)據(jù)![]() ,
,![]() ,…,
,…,![]() 的方差為2,則數(shù)據(jù)
的方差為2,則數(shù)據(jù)![]() ,
,![]() ,…,
,…,![]() 的方差為16.
的方差為16.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】函數(shù)![]() ,
,![]() ,
,![]() .
.
(1)設![]() ,假設
,假設![]() 在
在![]() 上遞減,求
上遞減,求![]() 的取值范圍;
的取值范圍;
(2)假設![]() ,求證:
,求證:![]() .
.
(3)是否存在實數(shù)![]() ,使得
,使得![]() 恒成立,假設存在,求出
恒成立,假設存在,求出![]() 的取值范圍,假設不存在,請說明理由.
的取值范圍,假設不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() ,
,![]() ,
,![]() .
.
(1)求函數(shù)![]() 的單調(diào)增區(qū)間;
的單調(diào)增區(qū)間;
(2)令![]() ,且函數(shù)
,且函數(shù)![]() 有三個彼此不相等的零點
有三個彼此不相等的零點![]() ,其中
,其中![]() .
.
①若![]() ,求函數(shù)
,求函數(shù)![]() 在
在![]() 處的切線方程;
處的切線方程;
②若對![]() ,
,![]() 恒成立,求實數(shù)
恒成立,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某工廠生產(chǎn)的產(chǎn)品中分正品與次品,正品重![]() ,次品重
,次品重![]() ,現(xiàn)有5袋產(chǎn)品(每袋裝有10個產(chǎn)品),已知其中有且只有一袋次品(10個產(chǎn)品均為次品)如果將5袋產(chǎn)品以1~5編號,第
,現(xiàn)有5袋產(chǎn)品(每袋裝有10個產(chǎn)品),已知其中有且只有一袋次品(10個產(chǎn)品均為次品)如果將5袋產(chǎn)品以1~5編號,第![]() 袋取出
袋取出![]() 個產(chǎn)品(
個產(chǎn)品(![]() ),并將取出的產(chǎn)品一起用秤(可以稱出物體重量的工具)稱出其重量
),并將取出的產(chǎn)品一起用秤(可以稱出物體重量的工具)稱出其重量![]() ,若次品所在的袋子的編號是2,此時的重量
,若次品所在的袋子的編號是2,此時的重量![]() _________
_________![]() ;若次品所在的袋子的編號是
;若次品所在的袋子的編號是![]() ,此時的重量
,此時的重量![]() _______
_______![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在直角坐標系![]() 中,曲線
中,曲線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù)),以坐標原點為極點,
為參數(shù)),以坐標原點為極點,![]() 軸正半軸為極軸的建立極坐標系,曲線
軸正半軸為極軸的建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求曲線![]() 的普通方程;
的普通方程;
(2)若點![]() 與點
與點![]() 分別為曲線
分別為曲線![]() 動點,求
動點,求![]() 的最小值,并求此時的
的最小值,并求此時的![]() 點坐標.
點坐標.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】博覽會安排了分別標有序號為“1號”“2號”“3號”的三輛車,等可能隨機順序前往酒店接嘉賓.某嘉賓突發(fā)奇想,設計兩種乘車方案.方案一:不乘坐第一輛車,若第二輛車的車序號大于第一輛車的車序號,就乘坐此車,否則乘坐第三輛車;方案二:直接乘坐第一輛車.記方案一與方案二坐到“3號”車的概率分別為P1,P2,則( )
A. P1P2=![]() B. P1=P2=
B. P1=P2=![]() C. P1+P2=
C. P1+P2=![]() D. P1<P2
D. P1<P2
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
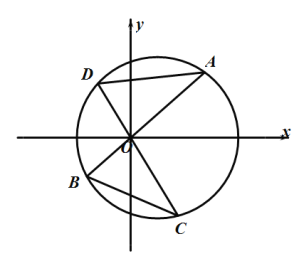
【題目】已知圓![]() ,線段
,線段![]() 、
、![]() 都是圓
都是圓![]() 的弦,且
的弦,且![]() 與
與![]() 垂直且相交于坐標原點
垂直且相交于坐標原點![]() ,如圖所示,設△
,如圖所示,設△![]() 的面積為
的面積為![]() ,設△
,設△![]() 的面積為
的面積為![]() .
.
(1)設點![]() 的橫坐標為
的橫坐標為![]() ,用
,用![]() 表示
表示![]() ;
;
(2)求證:![]() 為定值;
為定值;
(3)用![]() 、
、![]() 、
、![]() 、
、![]() 表示出
表示出![]() ,試研究
,試研究![]() 是否有最小值,如果有,求出最小值,并寫出此時直線
是否有最小值,如果有,求出最小值,并寫出此時直線![]() 的方程;若沒有最小值,請說明理由.
的方程;若沒有最小值,請說明理由.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com