
【題目】已知函數f(x)=(1﹣sinx)ex.
(1)求f(x)在區間(0,π)的極值;
(2)證明:函數g(x)=f(x)﹣sinx﹣1在區間(﹣π,π)有且只有3個零點,且之和為0.
【答案】(1)極小值![]() ,無極大值;(2)見解析
,無極大值;(2)見解析
【解析】
(1)先對函數進行求導,再根據導函數的零點進行分類討論即可;
(2)先求出0是![]() 的一個零點,然后判斷出
的一個零點,然后判斷出![]() 在
在![]() 上的單調性,結合第(1)問,得出
上的單調性,結合第(1)問,得出![]() 在
在![]() 上的單調性,進而得出
上的單調性,進而得出![]() 在
在![]() 只有一個零點
只有一個零點![]() ;通過求
;通過求![]() ,可以得到
,可以得到![]() 在
在![]() 上也只有一個零點
上也只有一個零點![]() ;從而證明函數
;從而證明函數![]() 在區間
在區間![]() 有且只有3個零點,且之和為0.
有且只有3個零點,且之和為0.
(1)因為![]() ,
,
所以![]() ,
,
令![]() ,得
,得![]() ,
,![]() ,從而
,從而![]() ,
,
當![]() 時,
時,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,從而
,從而![]() 單調遞減;
單調遞減;
當![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,從而
,從而![]() 單調遞增,
單調遞增,
故![]() 在區間
在區間![]() 有極小值
有極小值![]() ,無極大值;
,無極大值;
(2)證明:因為![]() ,所以
,所以![]() ,從而
,從而![]() 是
是![]() 的一個零點;
的一個零點;
令![]() ,則
,則![]() 在區間
在區間![]() 單調遞減,在區間
單調遞減,在區間![]() 單調遞增,
單調遞增,
所以![]() 在區間
在區間![]() 單調遞減,在區間
單調遞減,在區間![]() 單調遞增,
單調遞增,
又![]() ,
,![]() ,
,
所以![]() 在區間
在區間![]() 有唯一的零點,記為
有唯一的零點,記為![]() ,
,
又因為![]()
![]() ,
,
所以對于任意的![]() ,若
,若![]() ,必有
,必有![]() ,
,
所以![]() 在區間
在區間![]() 有唯一的零點
有唯一的零點![]() ,
,
故![]() 在區間
在區間![]() 的零點為
的零點為![]() ,0,
,0,![]() ,
,
所以![]() 在區間
在區間![]() 有且只有3個零點,且之和為0.
有且只有3個零點,且之和為0.


 一本好題口算題卡系列答案
一本好題口算題卡系列答案科目:高中數學 來源: 題型:
【題目】圓周率是圓的周長與直徑的比值,一般用希臘字母![]() 表示.早在公元480年左右,南北朝時期的數學家祖沖之就得出精確到小數點后7位的結果,他是世界上第一個把圓周率的數值計算到小數點后第7位的人,這比歐洲早了約1000年.生活中,我們也可以通過如下隨機模擬試驗來估計
表示.早在公元480年左右,南北朝時期的數學家祖沖之就得出精確到小數點后7位的結果,他是世界上第一個把圓周率的數值計算到小數點后第7位的人,這比歐洲早了約1000年.生活中,我們也可以通過如下隨機模擬試驗來估計![]() 的值:在區間
的值:在區間![]() 內隨機取
內隨機取![]() 個數,構成
個數,構成![]() 個數對
個數對![]() ,設
,設![]() ,
,![]() 能與1構成鈍角三角形三邊的數對
能與1構成鈍角三角形三邊的數對![]() 有
有![]() 對,則通過隨機模擬的方法得到的
對,則通過隨機模擬的方法得到的![]() 的近似值為( )
的近似值為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】德國數學家萊布尼茲(1646年-1716年)于1674年得到了第一個關于π的級數展開式,該公式于明朝初年傳入我國.在我國科技水平業已落后的情況下,我國數學家天文學家明安圖(1692年-1765年)為提高我國的數學研究水平,從乾隆初年(1736年)開始,歷時近30年,證明了包括這個公式在內的三個公式,同時求得了展開三角函數和反三角函數的6個新級數公式,著有《割圓密率捷法》一書,為我國用級數計算π開創了先河.如圖所示的程序框圖可以用萊布尼茲“關于π的級數展開式”計算π的近似值(其中P表示π的近似值),若輸入![]() ,則輸出的結果是( )
,則輸出的結果是( )
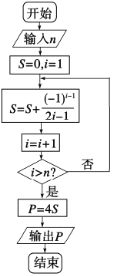
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖是我國2018年1月至12月石油進口量統計圖(其中同比是今年第![]() 個月與去年第
個月與去年第![]() 個月之比),則下列說法錯誤的是( )
個月之比),則下列說法錯誤的是( )

A.2018年下半年我國原油進口總量高于2018年上半年
B.2018年12個月中我國原油月最高進口量比月最低進口量高1152萬噸
C.2018年我國原油進口總量高于2017年我國原油進口總量
D.2018年1月—5月各月與2017年同期相比較,我國原油進口量有增有減
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某大型超市抽查了100天該超市的日純利潤數據,并將日純利潤數據分成以下幾組(單位:萬元):![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,統計結果如下表所示:
,統計結果如下表所示:
組別 |
|
|
|
|
|
|
頻數 | 5 | 20 | 30 | 30 | 10 | 5 |
以上述樣本分布的頻率估計總體分布的概率,解決下列問題:
(1)從該大型超市近幾年的銷售記錄中抽出5天,求其中日純利潤在區間![]() 內的天數不少于2的概率;
內的天數不少于2的概率;
(2)該超市經理由頻數分布表可以認為,該大型超市每天的純利潤![]() 服從正態分布
服從正態分布![]() ,其中,
,其中,![]() 近似為樣本平均數
近似為樣本平均數![]() (每組數據取區間的中點值).
(每組數據取區間的中點值).
①試利用該正態分布,估計該大型超市1000天內日純利潤在區間![]() 內的天數(精確到個位);
內的天數(精確到個位);
②該大型超市負責人根據每日的純利潤給超市員工制定了兩種不同的獎勵方案:
方案一:直接發放獎金,日純利潤低于![]() 時每名員工發放獎金70元,日純利潤不低于
時每名員工發放獎金70元,日純利潤不低于![]() 時每名員工發放獎金90元;
時每名員工發放獎金90元;
方案二:利用抽獎的方式獲得獎金,其中日純利潤不低于![]() 時每位員工均有兩次抽獎機會,日純利潤低于
時每位員工均有兩次抽獎機會,日純利潤低于![]() 時每位員工只有一次抽獎機會;每次抽獎的獎金及對應的概率分別為
時每位員工只有一次抽獎機會;每次抽獎的獎金及對應的概率分別為
金額 | 50元 | 100元 |
概率 |
|
|
小張恰好為該大型超市的一名員工,則從數學期望的角度看,小張選擇哪種獎勵方案更有利?
參考數據:若![]() ,則
,則![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() 的參數方程為
的參數方程為![]() (其中
(其中![]() 為參數),以原點為極點,
為參數),以原點為極點,![]() 軸非負半軸為極軸建立極坐標系,則曲線
軸非負半軸為極軸建立極坐標系,則曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求圓![]() 的普通方程與
的普通方程與![]() 的直角坐標方程;
的直角坐標方程;
(2)點![]() 是曲線
是曲線![]() 上一點,由
上一點,由![]() 向圓
向圓![]() 引切線,切點分別為
引切線,切點分別為![]() ,求四邊形
,求四邊形![]() 面積的最小值.
面積的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】[選修 4-4]參數方程與極坐標系
在平面直角坐標系![]() 中,已知曲線
中,已知曲線![]() :
: ![]() ,以平面直角坐標系
,以平面直角坐標系![]() 的原點
的原點![]() 為極點,
為極點, ![]() 軸正半軸為極軸,取相同的單位長度建立極坐標系.已知直線
軸正半軸為極軸,取相同的單位長度建立極坐標系.已知直線 ![]() :
: ![]() .
.
(Ⅰ)試寫出直線![]() 的直角坐標方程和曲線
的直角坐標方程和曲線![]() 的參數方程;
的參數方程;
(Ⅱ)在曲線![]() 上求一點
上求一點![]() ,使點
,使點![]() 到直線
到直線![]() 的距離最大,并求出此最大值.
的距離最大,并求出此最大值.
[選修 4-5]不等式選講
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】圓周率是圓的周長與直徑的比值,一般用希臘字母![]() 表示.早在公元480年左右,南北朝時期的數學家祖沖之就得出精確到小數點后7位的結果,他是世界上第一個把圓周率的數值計算到小數點后第7位的人,這比歐洲早了約1000年.生活中,我們也可以通過如下隨機模擬試驗來估計
表示.早在公元480年左右,南北朝時期的數學家祖沖之就得出精確到小數點后7位的結果,他是世界上第一個把圓周率的數值計算到小數點后第7位的人,這比歐洲早了約1000年.生活中,我們也可以通過如下隨機模擬試驗來估計![]() 的值:在區間
的值:在區間![]() 內隨機取
內隨機取![]() 個數,構成
個數,構成![]() 個數對
個數對![]() ,設
,設![]() ,
,![]() 能與1構成鈍角三角形三邊的數對
能與1構成鈍角三角形三邊的數對![]() 有
有![]() 對,則通過隨機模擬的方法得到的
對,則通過隨機模擬的方法得到的![]() 的近似值為( )
的近似值為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com