Question

14．已知函數f（x）=|log₂x|，g（x）=$\left\{{\begin{array}{l}{0，0＜x≤1}\\{\frac{1}{8}|{{x^2}-9}|，x＞1}\end{array}}$，若方程f（x）-g（x）=1在[a，+∞）上有三個實根，則正實數a的取值范圍為（0，$\frac{1}{2}$]．

Answer 1

分析 將方程f（x）-g（x）=1有三個實根轉化為函數y=f（x）-1與y=g（x）的圖象有三個交點，畫出兩個函數的圖象，然后根據圖象確定a的取值范圍

解答 ∵f（x）-g（x）=1在[a，+∞）上有三個實根
∴f（x）-1=g（x）在[a，+∞）上有三個實根
∴函數y=f（x）-1與y=g（x）的圖象在x∈[a，+∞）上有三個交點
作出y=f（x）-1和y=g（x）的圖象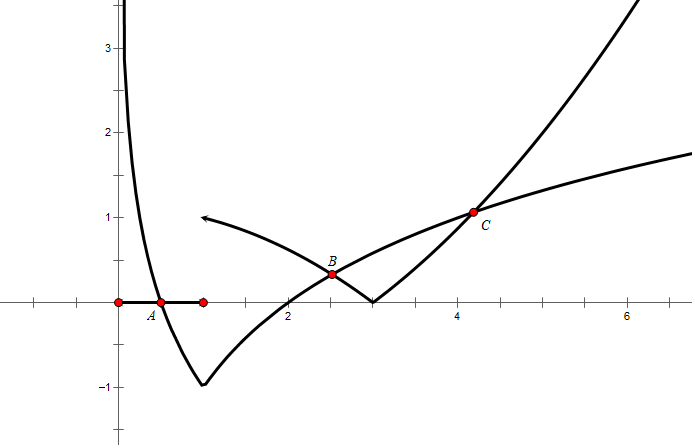

從圖象可知，0＜x_A＜1，y_A=0；x_B＞1，x_C＞1
令f（x）-1=|log₂x|-1=0，得x=$\frac{1}{2}$，或x=2，故${x}_{A}=\frac{1}{2}$
∴$a≤\frac{1}{2}$
又∵a為正實數
∴$0＜a≤\frac{1}{2}$，
故答案為：$（0，\frac{1}{2}]$

點評 本題考查了方程根的個數問題以及分段函數的圖象，將方程根的個數轉化為兩函數圖象交點的個數，從而利用數形結合思想求出a的取值范圍，屬于基礎題．