
【題目】如圖,D是直角△ABC斜邊BC上一點,AC= ![]() DC.
DC. 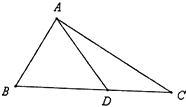
(Ⅰ)若∠DAC=30°,求角B的大小;
(Ⅱ)若BD=2DC,且AD= ![]() ,求DC的長.
,求DC的長.
【答案】解:(Ⅰ)在△ABC中,根據正弦定理,有 ![]() =
= ![]() . ∵AC=
. ∵AC= ![]() DC,∴sin∠ADC=
DC,∴sin∠ADC= ![]() =
= ![]() .
.
又∠ADC=∠B+∠BAD=∠B+60°>60° ,
∴∠ADC=120°.
于是∠C=180°﹣120°﹣30°=30° , ∴∠B=60°.
(Ⅱ)設DC=x,則BD=2x,BC=3x,AC= ![]() x.
x.
于是sinB= ![]() =
= ![]() ,cosB=
,cosB= ![]() ,AB=
,AB= ![]() x.
x.
在△ABD中,由余弦定理,AD2=AB2+BD2﹣2ABBDcosB,
即 ![]() ,得x=1.故DC=1
,得x=1.故DC=1
【解析】(Ⅰ)利用正弦定理、外角性質、三角形內角和定理即可得出.(Ⅱ)設DC=x,則BD=2x,BC=3x,AC= ![]() x.于是sinB=
x.于是sinB= ![]() =
= ![]() ,cosB=
,cosB= ![]() ,AB=
,AB= ![]() x.再利用余弦定理即可得出.
x.再利用余弦定理即可得出.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】公元263年左右,我國數學家劉徽發現當圓內接正多邊形的邊數無限增加時,多邊形面積可無限逼近圓的面積,并創立了“割圓術”,利用“割圓術”劉徽得到了圓周率精確到小數點后兩位的近似值![]() ,這就是著名的“徽率”,如圖是利用劉徽的“割圓術”思想設計的一個程序框圖,則輸出
,這就是著名的“徽率”,如圖是利用劉徽的“割圓術”思想設計的一個程序框圖,則輸出![]() 的值為 ( )
的值為 ( )
(參考數據:![]() )
)
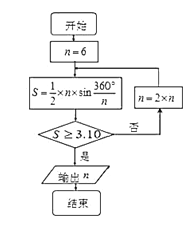
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某城市為了滿足市民出行的需要和節能環保的要求,在公共場所提供單車共享服務,某部門為了對該城市共享單車進行監管,隨機選取了![]() 位市民對共享單車的情況逬行問卷調査,并根根據其滿意度評分值(滿分
位市民對共享單車的情況逬行問卷調査,并根根據其滿意度評分值(滿分![]() 分)制作的莖葉圖如圖所示:
分)制作的莖葉圖如圖所示:
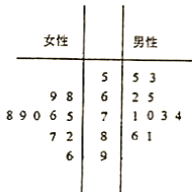
(1)分別計算男性打分的平均數和女性打分的中位數;
(2)從打分在![]() 分以下(不含
分以下(不含![]() 分)的市民抽取
分)的市民抽取![]() 人,求有女性被抽中的概率.
人,求有女性被抽中的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,四邊形
,四邊形![]() 為矩形,平面
為矩形,平面![]() 平面
平面![]() ,
, ![]() .
.
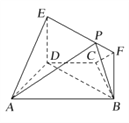
(Ⅰ)求證: ![]() 平面
平面![]() ;
;
(Ⅱ)點![]() 在線段
在線段![]() 上運動,設平面
上運動,設平面![]() 與平面
與平面![]() 所成銳二面角為
所成銳二面角為![]() ,試求
,試求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將函數y=sinx的圖象上所有點的橫坐標伸長到原來的2倍(縱坐標不變),再將所得的圖象向左平移 ![]() 個單位,得到的圖象對應的解析式是( )
個單位,得到的圖象對應的解析式是( )
A.y=sin(2x+ ![]() )
)
B.y=sin( ![]() x+
x+ ![]() )
)
C.y=sin( ![]() x+
x+ ![]() )
)
D.y=sin(2x+ ![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知各項不為零的數列![]() 的前
的前![]() 項和為
項和為![]() ,且
,且![]() ,
, ![]() ,
, ![]() .
.
(1)若![]() 成等比數列,求實數
成等比數列,求實數![]() 的值;
的值;
(2)若![]() 成等差數列,
成等差數列,
①求數列![]() 的通項公式;
的通項公式;
②在![]() 與
與![]() 間插入
間插入![]() 個正數,共同組成公比為
個正數,共同組成公比為![]() 的等比數列,若不等式
的等比數列,若不等式![]() 對任意的
對任意的![]() 恒成立,求實數
恒成立,求實數![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖是根據某班50名同學在某次數學測驗中的成績(百分制)繪制的概率分布直方圖,其中成績分組區間為:[40,50),[50,60),…,[80,90),[90,100]. 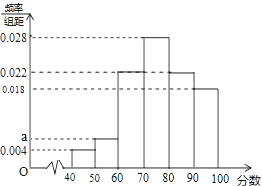
(1)求圖中a的值;
(2)計算該班本次的數學測驗成績不低于80分的學生的人數;
(3)根據頻率分布直方圖,估計該班本次數學測驗成績的平均數與中位數(要求中位數的估計值精確到0.1)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com