【題目】如圖，在梯形
中， 
， 
， 
，四邊形
為矩形，平面
平面
， 
.
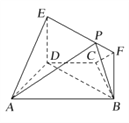
（Ⅰ）求證： 
平面
；
（Ⅱ）點
在線段
上運動，設平面
與平面
所成銳二面角為
，試求
的最小值.
閱讀快車系列答案科目：高中數學 來源： 題型：
【題目】在三棱錐ABC﹣A1B1C1中，底面ABC是邊長為2的正三角形，側棱AA1⊥底面ABC，AA1= 
，P、Q分別是AB、AC上的點，且PQ∥BC． 
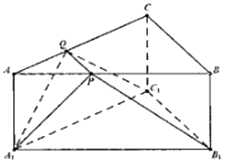
（1）若平面A1PQ與平面A1B1C1相交于直線l，求證：l∥B1C1；
（2）當平面A1PQ⊥平面PQC1B1時，確定點P的位置并說明理由．S．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下列命題：
①已知a，b，m都是正數，并且a＜b，則 
＞ 
；
②在△ABC中，角A，B，C的對邊分別為a，b，c，若∠A=60°，a=7，b=8，則三角形有一解；
③若函數f（x）= 
，則f（ 
）+f（ 
）+f（ 
）+…+f（ 
）=5；
④在等比數列{an}中，a1+a2+…+an= 
（其中n∈N* ， q為公比）；
⑤如圖，在正方體ABCD﹣A1B1C1D1中，點M，N分別是CD，CC1的中點，則異面直線A1M與DN所成角的大小是90°．
其中真命題有（寫出所有真命題的序號）．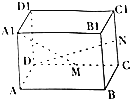
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系
中，過橢圓
右焦點
的直線
交
于
兩點 ， 
為
的中點，且
的斜率為
.
（1）求橢圓
的標準方程；
（2）設過點
的直線
（不與坐標軸垂直）與橢圓交于
兩點，若在線段
上存在點
，
使得
，求
的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，D是直角△ABC斜邊BC上一點，AC= 
DC．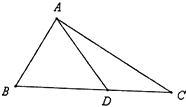 
（Ⅰ）若∠DAC=30°，求角B的大小；
（Ⅱ）若BD=2DC，且AD= 
，求DC的長．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖所示,在三棱柱ABC-A1B1C1中,AA1B1B為正方形,BB1C1C為菱形,B1CAC1
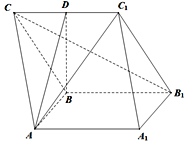
（Ⅰ）求證：平面AA1B1B面BB1C1C；
（Ⅱ）若D是CC1中點,ADB是二面角A-CC1-B的平面角,求直線AC1與平面ABC所成角的余弦值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】本市某玩具生產公司根據市場調查分析，決定調整產品生產方案，準備每天生產
， 
， 
三種玩具共100個，且
種玩具至少生產20個，每天生產時間不超過10小時，已知生產這些玩具每個所需工時（分鐘）和所獲利潤如表：
玩具名稱 |
|
|
|
工時（分鐘） | 5 | 7 | 4 |
利潤（元） | 5 | 6 | 3 |
（Ⅰ）用每天生產
種玩具個數
與
種玩具
表示每天的利潤
（元）；
（Ⅱ）怎樣分配生產任務才能使每天的利潤最大，最大利潤是多少？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
