
寒假期間,我市某校學生會組織部分同學,用“10分制”隨機調查“陽光花園”社區人們的幸福度,現從調查人群中隨機抽取16名,如果所示的莖葉圖記錄了他們的幸福度分數(以小數點前的一位數字為莖,小數點后的一位數字為葉);若幸福度分數不低于8.5分,則該人的幸福度為“幸福”.
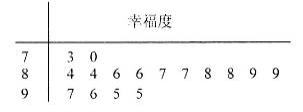
(1)求從這16人中隨機選取3人,至少有2人為“幸福”的概率;
(2)以這16人的樣本數據來估計整個社區的總體數據,若從該社區(人數很多)任選3人,記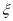 表示抽到“幸福”的人數,求
表示抽到“幸福”的人數,求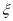 的分布列及數學期望.
的分布列及數學期望.
(1) (2)
(2)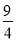
【解析】
試題分析:
(1)首先通過莖葉圖分析可得16人中,幸福的人有12人,則考慮通過計算事件這16人中隨機選取3人,至少有2人為“幸福”的對立事件,即從這16人中隨機抽取3人,至多1人是幸福的,也就是抽取的3人的只有1人或者沒有人是幸福的,利用組合數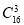 計算得到16抽取3人的所有的基本事件,再分步計數原理用組合數
計算得到16抽取3人的所有的基本事件,再分步計數原理用組合數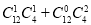 計算得到對立事件所包含的基本事件,再利用古典概型的概率計算公式即可得到對立事件的概率,則所求事件的概率為1減去對立事件的概率.
計算得到對立事件所包含的基本事件,再利用古典概型的概率計算公式即可得到對立事件的概率,則所求事件的概率為1減去對立事件的概率.
(2)因為16人中有12人是幸福的,即該社區中幸福的人占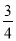 ,非幸福人數占
,非幸福人數占 ,有題可得可得
,有題可得可得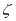 的取值可以是0,1,2,3,則利用獨立試驗同時發生的概率計算公式可以得到
的取值可以是0,1,2,3,則利用獨立試驗同時發生的概率計算公式可以得到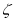 分別為0,1,2,3時所對應的概率,即可得到分布列,再把
分別為0,1,2,3時所對應的概率,即可得到分布列,再把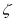 的值域對應概率相乘之和即可得到期望.
的值域對應概率相乘之和即可得到期望.
試題解析:
(1)記至少有2人是“幸福”為事件 ,由題意知
,由題意知
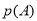 =1-
=1-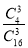 -
- =1-
=1-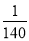 -
-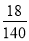 =
= ; 6分
; 6分
(2) 的可能取值為0,1,2,3.
的可能取值為0,1,2,3.
 ,
,
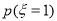
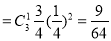 ,
,
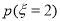
 ,
,
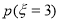
 , 10分
, 10分
所以 的分布列為:
的分布列為:
|
|
|
|
|
|
|
|
|
|
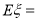
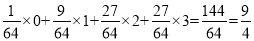 12分
12分
考點:分布列期望莖葉圖


科目:高中數學 來源:2013-2014學年山東省濟南市高三3月考模擬考試理科數學試卷(解析版) 題型:選擇題
某幾何體三視圖如圖所示,則該幾何體的體積等于( )
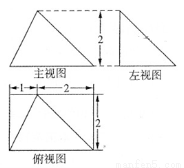
(A)2 (B)4
(C)8 (D)12
查看答案和解析>>
科目:高中數學 來源:2013-2014學年山東省日照市高三5月統一質量檢測考試理科數學試卷(解析版) 題型:選擇題
在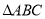 中,角A,B,C的對邊分別為
中,角A,B,C的對邊分別為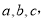 若
若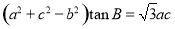 ,則角B的值為( )
,則角B的值為( )
A.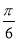 B.
B.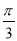 C.
C.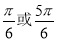 D.
D.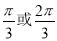
查看答案和解析>>
科目:高中數學 來源:2013-2014學年山東省日照市高三5月統一質量檢測考試文科數學試卷(解析版) 題型:選擇題
已知P,Q為圓 :
: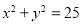 上的任意兩點,且
上的任意兩點,且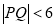 ,若線段PQ的中點組成的區域為M,在圓O內任取一點,則該點落在區域M內的概率為( )
,若線段PQ的中點組成的區域為M,在圓O內任取一點,則該點落在區域M內的概率為( )
A.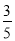 B.
B. C.
C.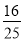 D.
D.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年山東省日照市高三3月第一次模擬考試理科數學試卷(解析版) 題型:填空題
執行右面的框圖,若輸出p的值是24,則輸入的正整數N應為________.

查看答案和解析>>
科目:高中數學 來源:2013-2014學年山東省日照市高三3月第一次模擬考試理科數學試卷(解析版) 題型:選擇題
“ ”是“
”是“ ”的( )
”的( )
A.充分不必要條件 B.必要不充分條件
C.充要條件 D.既不充分也不必要條件
查看答案和解析>>
科目:高中數學 來源:2013-2014學年山東省日照市高三3月第一次模擬考試文科數學試卷(解析版) 題型:選擇題
已知定義在R上的函數 滿足條件;①對任意的
滿足條件;①對任意的 ,都有
,都有 ;②對任意的
;②對任意的 ;③函數
;③函數 的圖象關于y軸對稱.則下列結論正確的是( )
的圖象關于y軸對稱.則下列結論正確的是( )
A. B.
B.
C. D.
D.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年山東省東營市高三4月統一質量檢測考試理科數學試卷(解析版) 題型:解答題
設數列 為等差數列,且
為等差數列,且 ,
, ,數列
,數列 的前
的前 項和為
項和為 ,
, 且
且 .
.
(1)求數列 ,
, 的通項公式;
的通項公式;
(2)若 ,
, 為數列
為數列 的前
的前 項和,
項和, 對
對 恒成立,求
恒成立,求 的最小值.
的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com