
【題目】如圖,在多面體ABCDEF中,四邊形ABCD為菱形,且![]() ,
,![]() 平面ABCD,
平面ABCD,![]() ,且
,且![]() ,
,![]() .
.
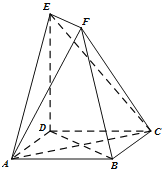
![]() Ⅰ
Ⅰ![]() 求證:
求證:![]() 平面ACF;
平面ACF;
![]() Ⅱ
Ⅱ![]() 求直線AE與平面ACF所成角的正弦值.
求直線AE與平面ACF所成角的正弦值.
【答案】(Ⅰ)詳見解析;(Ⅱ)![]() .
.
【解析】
![]() Ⅰ
Ⅰ![]() 取AC與BD的交點為O,連OF,證明
取AC與BD的交點為O,連OF,證明![]() ,且
,且![]() ,即可證明
,即可證明![]() ,進(jìn)而得到
,進(jìn)而得到![]() 平面ACF;
平面ACF;
![]() Ⅱ
Ⅱ![]() 將線面角轉(zhuǎn)化為
將線面角轉(zhuǎn)化為![]() ,或者建立坐標(biāo)系,用向量法處理.
,或者建立坐標(biāo)系,用向量法處理.
解:![]() Ⅰ
Ⅰ![]() 證明:取AC與BD的交點為O,連OF,
證明:取AC與BD的交點為O,連OF,
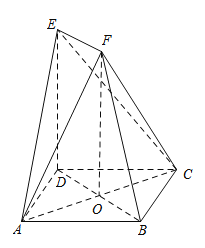
![]() ,
,![]() ,
,
![]() 四邊形EFOD為平行四邊形,
四邊形EFOD為平行四邊形,
![]() ,
,
![]() 平面
平面![]() 平面AFC,
平面AFC,
![]() 平面ACF;
平面ACF;
![]() Ⅱ
Ⅱ![]() 解法一:
解法一:![]() 平面ABCD,
平面ABCD,
![]() ,又
,又![]() ,
,![]()
![]() 四邊形ABCD為菱形,
四邊形ABCD為菱形,![]()
![]() ,
,
![]() 平面ACF,
平面ACF,
![]() 是直線AE與平面ACF所成角,
是直線AE與平面ACF所成角,
可得![]() ,
,![]() ,
,![]() ,
,
![]() .
.
方法二:易證OA,OB,OF兩兩垂直,以OA,OB,OF所在直線分別為x,y,z軸建系,如圖,

![]() ,
,
![]()
設(shè)平面ACF法向量為 ,
,
得一個法向量![]() ,
,
![]() ,
,
直線AE與平面ACF所成角的正弦值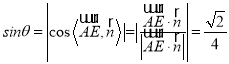 .
.


 學(xué)練快車道快樂假期寒假作業(yè)系列答案
學(xué)練快車道快樂假期寒假作業(yè)系列答案 新思維寒假作業(yè)系列答案
新思維寒假作業(yè)系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】某籃球隊甲、乙兩名運(yùn)動員練習(xí)罰球,每人練習(xí)10組,每組罰球40個.命中個數(shù)的莖葉圖如圖,則下面結(jié)論中錯誤的一個是( )

A. 甲的極差是29 B. 甲的中位數(shù)是24
C. 甲罰球命中率比乙高 D. 乙的眾數(shù)是21
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平面直角坐標(biāo)系xOy中,![]() ,
,![]() 分別是橢圓
分別是橢圓![]() 的左,右焦點,點P是橢圓E上一點,滿足
的左,右焦點,點P是橢圓E上一點,滿足![]() 軸,
軸,![]() .
.
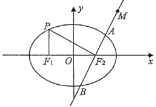
(1)求橢圓E的離心率;
(2)過點![]() 的直線l與橢圓E交于兩點A,B,若在橢圓B上存在點Q,使得四邊形OAQB為平行四邊形,求直線l的斜率.
的直線l與橢圓E交于兩點A,B,若在橢圓B上存在點Q,使得四邊形OAQB為平行四邊形,求直線l的斜率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,棱錐P—ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,BD=![]() .
.
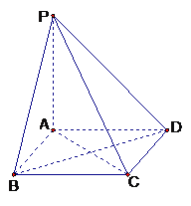
(1)求證:BD⊥平面PAC;
(2)求二面角P—CD—B余弦值的大小;
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】橢圓![]() 的離心率為
的離心率為![]() 且四個頂點構(gòu)成面積為
且四個頂點構(gòu)成面積為![]() 的菱形.
的菱形.
(Ⅰ)求橢圓的標(biāo)準(zhǔn)方程;
(Ⅱ)過點![]() 且斜率不為0的直線
且斜率不為0的直線![]() 與橢圓交于
與橢圓交于![]() ,
,![]() 兩點,記
兩點,記![]() 中點為
中點為![]() ,坐標(biāo)原點為
,坐標(biāo)原點為![]() ,直線
,直線![]() 交橢圓于
交橢圓于![]() ,
,![]() 兩點,當(dāng)四邊形
兩點,當(dāng)四邊形![]() 的面積為
的面積為![]() 時,求直線
時,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)函數(shù)![]() ,其中
,其中![]() 為正實數(shù).
為正實數(shù).
(Ⅰ)若![]() 是函數(shù)
是函數(shù)![]() 的極值點,討論函數(shù)
的極值點,討論函數(shù)![]() 的單調(diào)性;
的單調(diào)性;
(Ⅱ)若![]() 在
在![]() 上無最小值,且
上無最小值,且![]() 在
在![]() 上是單調(diào)增函數(shù),求
上是單調(diào)增函數(shù),求![]() 的取值范圍,并由此判斷曲線
的取值范圍,并由此判斷曲線![]() 與曲線
與曲線![]() 在
在![]() 交點個數(shù).
交點個數(shù).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】6月12日,上海市發(fā)布了《上海市生活垃圾分類投放指南》,將人們生活中產(chǎn)生的大部分垃圾分為七大類.某幢樓前有四個垃圾桶,分別標(biāo)有“可回收物”、“有害垃圾”、“濕垃圾”、“干垃圾”,小明同學(xué)要將雞骨頭(濕垃圾)、貝殼(干垃圾)、指甲油(有害垃圾)、報紙(可回收物)全部投入到這四個桶中,若每種垃圾投放到每個桶中都是等可能的,那么隨機(jī)事件“4種垃圾中至少有2種投入正確的桶中”的概率是______.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某區(qū)選派7名隊員代表本區(qū)參加全市青少年圍棋錦標(biāo)賽,其中3名來自A學(xué)校且1名為女棋手,另外4名來自B學(xué)校且2名為女棋手![]() 從這7名隊員中隨機(jī)選派4名隊員參加第一階段的比賽
從這7名隊員中隨機(jī)選派4名隊員參加第一階段的比賽
![]() 求在參加第一階段比賽的隊員中,恰有1名女棋手的概率;
求在參加第一階段比賽的隊員中,恰有1名女棋手的概率;
![]() Ⅱ
Ⅱ![]() 設(shè)X為選出的4名隊員中A、B兩校人數(shù)之差的絕對值,求隨機(jī)變量X的分布列和數(shù)學(xué)期望
設(shè)X為選出的4名隊員中A、B兩校人數(shù)之差的絕對值,求隨機(jī)變量X的分布列和數(shù)學(xué)期望
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)函數(shù)![]() ,
, ![]() ,
, ![]() 為自然對數(shù)的底數(shù).
為自然對數(shù)的底數(shù).
(Ⅰ)若函數(shù)![]() 存在兩個零點,求
存在兩個零點,求![]() 的取值范圍;
的取值范圍;
(Ⅱ)若對任意![]() ,
, ![]() ,
, ![]() 恒成立,求實數(shù)
恒成立,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com