

解:在△AOB中,設OA=a,OB=b,
∵AO為正東方向,OB為東北方向,
∴∠AOB=135°.
∴|AB|2=a2+b2-2abcos135°=a2+b2+![]() ab.
ab.
又O到AB的距離為10,
設∠OAB=α(0°<α<45°),
則∠OBA=45°-α.
∴a=![]() ,b=
,b=![]() .∴|AB|2=
.∴|AB|2=![]() +
+![]() +
+![]() ·
·![]() ·
·![]() =
=
100·![]() =
=![]()
=![]() =
=![]() .
.
∴0°<α<45°,
∴45°<2α+45°<135°.
∴![]() <sin(2α+45°)≤1.
<sin(2α+45°)≤1.
∴|AB|2≥![]() =400(
=400(![]() +1)2(當且僅當α=22.5°時取等號).
+1)2(當且僅當α=22.5°時取等號).
∴|AB|min=20(![]() +1).
+1).
此時,a=b=![]() =10
=10![]() ,
,
即當A、B離O點均為10![]() km時,能使|AB|最短.其最短距離為20(
km時,能使|AB|最短.其最短距離為20(![]() +1) km.
+1) km.


科目:高中數學 來源: 題型:
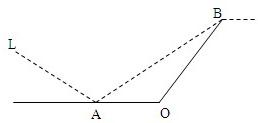 某城市有一條公路,自西向東經過A點到市中心O點后轉向東北方向OB,現要修建一條鐵路L,L在OA上設一站A,在OB上設一站B,鐵路在AB部分為直線段,現要求市中心O與AB的距離為10 km,問把A、B分別設在公路上離中心O多遠處才能使|AB|最短?并求其最短距離.
某城市有一條公路,自西向東經過A點到市中心O點后轉向東北方向OB,現要修建一條鐵路L,L在OA上設一站A,在OB上設一站B,鐵路在AB部分為直線段,現要求市中心O與AB的距離為10 km,問把A、B分別設在公路上離中心O多遠處才能使|AB|最短?并求其最短距離.查看答案和解析>>
科目:高中數學 來源: 題型:
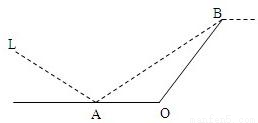
某城市有一條公路,自西向東經過A點到市中心O點后轉向東北方向OB,現要修建一條鐵路L,L在OA上設一站A,在OB上設一站B,鐵路在AB部分為直線段,現要求市中心O與AB的距離為10 km, 問把A、B分別設在公路上離中心O多遠處才能使|AB|最短?并求其最短距離.
問把A、B分別設在公路上離中心O多遠處才能使|AB|最短?并求其最短距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源:2006年高考第一輪復習數學:5.4 解斜三角形(解析版) 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com