
【題目】定義![]() (
(![]() ,
,![]() )為有限實(shí)數(shù)列
)為有限實(shí)數(shù)列![]() 的波動強(qiáng)度.
的波動強(qiáng)度.
(1)求數(shù)列1,4,2,3的波動強(qiáng)度;
(2)若數(shù)列![]() ,
,![]() ,
,![]() ,
,![]() 滿足
滿足![]() ,判斷
,判斷![]() 是否正確,如果正確請證明,如果錯誤請舉出反例;
是否正確,如果正確請證明,如果錯誤請舉出反例;
(3)設(shè)數(shù)列![]() ,
,![]() ,
,![]() ,
,![]() 是數(shù)列
是數(shù)列![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的一個排列,求
的一個排列,求![]() 的最大值,并說明理由.
的最大值,并說明理由.
【答案】(1)![]() (2)
(2)![]() 是正確的,詳見解析(3)當(dāng)
是正確的,詳見解析(3)當(dāng)![]() 為偶數(shù)時,
為偶數(shù)時,![]() ,
,![]()
![]() ;當(dāng)
;當(dāng)![]() 為奇數(shù)時,
為奇數(shù)時,![]() ,
,![]()
![]()
【解析】
(1)根據(jù)波動強(qiáng)度的定義直接計算;
(2)作差![]() ,利用
,利用![]() 或
或![]() 判斷正負(fù)即可;
判斷正負(fù)即可;
(3)設(shè)![]() ,
,![]() ,
,![]() 是單調(diào)遞增數(shù)列,可整理
是單調(diào)遞增數(shù)列,可整理![]() ,其中
,其中![]() ,
,![]() ,并且
,并且![]() .經(jīng)過上述調(diào)整后的數(shù)列,系數(shù)
.經(jīng)過上述調(diào)整后的數(shù)列,系數(shù)![]() 不可能為0,分
不可能為0,分![]() 的奇偶性討論,確定各自含有的
的奇偶性討論,確定各自含有的![]() 的個數(shù),進(jìn)而求出
的個數(shù),進(jìn)而求出![]() 的最大值.
的最大值.
解:(1)![]()
(2)![]() 是正確的
是正確的
證明:![]()
![]()
![]() 或
或![]() ,
,
![]() 且
且![]()
![]()
所以![]() ,即
,即![]()
并且當(dāng)![]() 時,
時,![]() 可以取等號,當(dāng)
可以取等號,當(dāng)![]() 時,
時,![]() 可以取等號,
可以取等號,
所以等號可以取到;
(3)設(shè)![]() ,
,![]() ,
,![]() 是單調(diào)遞增數(shù)列.
是單調(diào)遞增數(shù)列.
分![]() 是奇、偶數(shù)情況討論
是奇、偶數(shù)情況討論
![]() ,其中
,其中![]() ,
,![]() ,并且
,并且![]() .經(jīng)過上述調(diào)整后的數(shù)列,系數(shù)
.經(jīng)過上述調(diào)整后的數(shù)列,系數(shù)![]() 不可能為0.
不可能為0.
當(dāng)![]() 為偶數(shù)時,系數(shù)中有
為偶數(shù)時,系數(shù)中有![]() 個
個![]() 和
和![]() 個
個![]() ,
,![]() 個
個![]() 和
和![]() 個
個![]() .
.
當(dāng)![]() 為奇數(shù)時,有兩種情況:系數(shù)中有
為奇數(shù)時,有兩種情況:系數(shù)中有![]() 個
個![]() 和
和![]() 個
個![]() ,
,![]() 個
個![]() ;
;
或系數(shù)中有![]() 個
個![]() 和
和![]() 個
個![]() ,
,![]() 個
個![]() .
.
[1]![]() 是偶數(shù),
是偶數(shù),![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]()
[2]![]() 是奇數(shù),
是奇數(shù),![]() ,
,
因為![]() ,
,![]() ,可知
,可知
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
綜上,當(dāng)![]() 為偶數(shù)時,
為偶數(shù)時,![]() ,
,![]()
![]() ;
;
當(dāng)![]() 為奇數(shù)時,
為奇數(shù)時,![]() ,
,![]()
![]()


 開心快樂假期作業(yè)暑假作業(yè)西安出版社系列答案
開心快樂假期作業(yè)暑假作業(yè)西安出版社系列答案 名題訓(xùn)練系列答案
名題訓(xùn)練系列答案 期末集結(jié)號系列答案
期末集結(jié)號系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】下列判斷正確的是( )
A.“![]() ”是“
”是“![]() ”的充分不必要條件
”的充分不必要條件
B.函數(shù)![]() 的最小值為2
的最小值為2
C.當(dāng)![]() 時,命題“若
時,命題“若![]() ,則
,則![]() ”為真命題
”為真命題
D.命題“![]() ,
,![]() ”的否定是“
”的否定是“![]() ,
,![]() ”
”
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,正方體![]() 的棱長為2,P是BC的中點(diǎn),點(diǎn)Q是棱
的棱長為2,P是BC的中點(diǎn),點(diǎn)Q是棱![]() 上的動點(diǎn).
上的動點(diǎn).
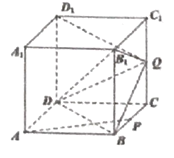
(1)點(diǎn)Q在何位置時,直線![]() ,DC,AP交于一點(diǎn),并說明理由;
,DC,AP交于一點(diǎn),并說明理由;
(2)求三棱錐![]() 的體積;
的體積;
(3)棱![]() 上是否存在動點(diǎn)Q,使得
上是否存在動點(diǎn)Q,使得![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() ,若存在指出點(diǎn)Q在棱
,若存在指出點(diǎn)Q在棱![]() 上的位置,若不存在,請說明理由.
上的位置,若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)求證:函數(shù)![]() 是偶函數(shù);
是偶函數(shù);
(2)設(shè)![]() ,求關(guān)于
,求關(guān)于![]() 的函數(shù)
的函數(shù)![]() 在
在![]() 時的值域
時的值域![]() 的表達(dá)式;
的表達(dá)式;
(3)若關(guān)于![]() 的不等式
的不等式![]() 在
在![]() 時恒成立,求實(shí)數(shù)
時恒成立,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】選修4-4:坐標(biāo)系與參數(shù)方程:在直角坐標(biāo)系![]() 中,曲線
中,曲線![]() (
(![]() 為參數(shù)),以坐標(biāo)原點(diǎn)
為參數(shù)),以坐標(biāo)原點(diǎn)![]() 為極點(diǎn),以
為極點(diǎn),以![]() 軸的正半軸為極軸建立極坐標(biāo)系,曲線
軸的正半軸為極軸建立極坐標(biāo)系,曲線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() .
.
(1)求曲線![]() 的極坐標(biāo)方程;
的極坐標(biāo)方程;
(2)已知點(diǎn)![]() ,直線
,直線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() ,它與曲線
,它與曲線![]() 的交點(diǎn)為
的交點(diǎn)為![]() ,
,![]() ,與曲線
,與曲線![]() 的交點(diǎn)為
的交點(diǎn)為![]() ,求
,求![]() 的面積.
的面積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖1,在正方形![]() 中,
中,![]() 是
是![]() 的中點(diǎn),點(diǎn)
的中點(diǎn),點(diǎn)![]() 在線段
在線段![]() 上,且
上,且![]() .若將
.若將![]() 分別沿
分別沿![]() 折起,使
折起,使![]() 兩點(diǎn)重合于點(diǎn)
兩點(diǎn)重合于點(diǎn)![]() ,如圖2.
,如圖2.
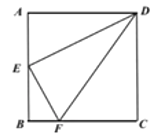
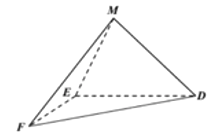
圖1 圖2
(1)求證:![]() 平面
平面![]() ;
;
(2)求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在直角坐標(biāo)系![]() 中,曲線
中,曲線![]() 的參數(shù)方程為
的參數(shù)方程為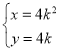 (
(![]() 為參數(shù)),以坐標(biāo)原點(diǎn)為極點(diǎn),
為參數(shù)),以坐標(biāo)原點(diǎn)為極點(diǎn),![]() 軸正半軸為極軸建立極坐標(biāo)系,直線
軸正半軸為極軸建立極坐標(biāo)系,直線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() .
.
(1)求直線![]() 和曲線
和曲線![]() 的普通方程;
的普通方程;
(2)已知點(diǎn)![]() ,且直線
,且直線![]() 和曲線
和曲線![]() 交于
交于![]() 兩點(diǎn),求
兩點(diǎn),求![]() 的值
的值
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某社區(qū)![]() 名居民參加
名居民參加![]() 年國慶活動,他們的年齡在
年國慶活動,他們的年齡在![]() 歲至
歲至![]() 歲之間,將年齡按
歲之間,將年齡按![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 分組,得到的頻率分布直方圖如圖所示.
分組,得到的頻率分布直方圖如圖所示.
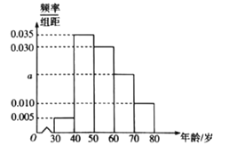
(1)求![]() 的值,并求該社區(qū)參加
的值,并求該社區(qū)參加![]() 年國慶活動的居民的平均年齡(每個分組取中間值作代表);
年國慶活動的居民的平均年齡(每個分組取中間值作代表);
(2)現(xiàn)從年齡在![]() 、
、![]() 的人員中按分層抽樣的方法抽取
的人員中按分層抽樣的方法抽取![]() 人,再從這
人,再從這![]() 人中隨機(jī)抽取
人中隨機(jī)抽取![]() 人進(jìn)行座談,用
人進(jìn)行座談,用![]() 表示參與座談的居民的年齡在
表示參與座談的居民的年齡在![]() 的人數(shù),求
的人數(shù),求![]() 的分布列和數(shù)學(xué)期望;
的分布列和數(shù)學(xué)期望;
(3)若用樣本的頻率代替概率,用隨機(jī)抽樣的方法從該地![]() 歲至
歲至![]() 歲之間的市民中抽取
歲之間的市民中抽取![]() 名進(jìn)行調(diào)查,其中有
名進(jìn)行調(diào)查,其中有![]() 名市民的年齡在
名市民的年齡在![]() 的概率為
的概率為![]() ,當(dāng)
,當(dāng)![]() 最大時,求
最大時,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com