
【題目】在直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為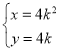 (
(![]() 為參數),以坐標原點為極點,
為參數),以坐標原點為極點,![]() 軸正半軸為極軸建立極坐標系,直線
軸正半軸為極軸建立極坐標系,直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求直線![]() 和曲線
和曲線![]() 的普通方程;
的普通方程;
(2)已知點![]() ,且直線
,且直線![]() 和曲線
和曲線![]() 交于
交于![]() 兩點,求
兩點,求![]() 的值
的值
科目:高中數學 來源: 題型:
【題目】若函數![]() 是定義在
是定義在![]() 上的奇函數,且當
上的奇函數,且當![]() 時,
時,![]() .
.
(Ⅰ)若![]() ,求函數
,求函數![]() 的解析式;
的解析式;
(Ⅱ)若![]() ,方程
,方程![]() 至少有兩個不等的解,求
至少有兩個不等的解,求![]() 的取值集合;
的取值集合;
(Ⅲ)若函數![]() 為
為![]() 上的單調減函數,
上的單調減函數,
①求![]() 的取值范圍;
的取值范圍;
②若不等式![]() 成立,求實數
成立,求實數![]() 的取值集合.
的取值集合.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】![]() 市實施全域旅游,將鄉村旅游公路建設與特色田園鄉村發展結合,精心打造全長365公里的“1號公路”,對內串聯區域內主要景區景點和自然村,對外通達周邊縣(市),以路引景、為景串線,形成一個“大環小圈、內連外引”的路網體系.如今的“1號公路”,不僅成為該市旅游業的“顏值擔當”,更成為推動鄉村振興的“實力擔當”,農村居住環境日益改善,新農村別墅隨處可見.圖①是一棟新農村別墅,它由上部屋頂和下部主體兩部分組成.如圖②,屋頂由四坡屋面構成,其中前后兩坡屋面
市實施全域旅游,將鄉村旅游公路建設與特色田園鄉村發展結合,精心打造全長365公里的“1號公路”,對內串聯區域內主要景區景點和自然村,對外通達周邊縣(市),以路引景、為景串線,形成一個“大環小圈、內連外引”的路網體系.如今的“1號公路”,不僅成為該市旅游業的“顏值擔當”,更成為推動鄉村振興的“實力擔當”,農村居住環境日益改善,新農村別墅隨處可見.圖①是一棟新農村別墅,它由上部屋頂和下部主體兩部分組成.如圖②,屋頂由四坡屋面構成,其中前后兩坡屋面![]() 和
和![]() 是全等的等腰梯形,左右兩坡屋面
是全等的等腰梯形,左右兩坡屋面![]() 和
和![]() 是全等的三角形.點
是全等的三角形.點![]() 在平面
在平面![]() 和
和![]() 上的射影分別為
上的射影分別為![]() (即:
(即:![]() 平面
平面![]() ,垂足為
,垂足為![]() ;
;![]() ,垂足為
,垂足為![]() ).已知
).已知![]() ,梯形
,梯形![]() 的面積是
的面積是![]() 面積的2.2倍.
面積的2.2倍.![]() .
.

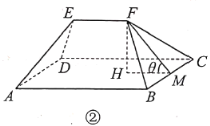
(1)當![]() 時,求屋頂面積的大小;
時,求屋頂面積的大小;
(2)求屋頂面積![]() 關于
關于![]() 的函數關系式;
的函數關系式;
(3)已知上部屋頂造價與屋頂面積成正比,比例系數為![]() (
(![]() 為正的常數),下部主體造價與其高度成正比,比例系數為
為正的常數),下部主體造價與其高度成正比,比例系數為![]() .現欲造一棟上、下總高度為
.現欲造一棟上、下總高度為![]() 的別墅,試問:當
的別墅,試問:當![]() 為何值時,總造價最低?
為何值時,總造價最低?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() (
(![]() ),
),![]() .
.
(1)若![]() 的圖象在
的圖象在![]() 處的切線恰好也是
處的切線恰好也是![]() 圖象的切線.
圖象的切線.
①求實數![]() 的值;
的值;
②若方程![]() 在區間
在區間![]() 內有唯一實數解,求實數
內有唯一實數解,求實數![]() 的取值范圍.
的取值范圍.
(2)當![]() 時,求證:對于區間
時,求證:對于區間![]() 上的任意兩個不相等的實數
上的任意兩個不相等的實數![]() ,
, ![]() ,都有
,都有![]() 成立.
成立.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=log4(4x+1)+kx與g(x)=log4(a2x﹣![]() a),其中f(x)是偶函數.
a),其中f(x)是偶函數.
(1)求實數k的值;
(2)求函數g(x)的定義域;
(3)若函數f(x)與g(x)的圖象有且只有一個公共點,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 中心在原點,焦點在坐標軸上,直線
中心在原點,焦點在坐標軸上,直線![]() 與橢圓
與橢圓![]() 在第一象限內的交點是
在第一象限內的交點是![]() ,點
,點![]() 在
在![]() 軸上的射影恰好是橢圓
軸上的射影恰好是橢圓![]() 的右焦點
的右焦點![]() ,橢圓
,橢圓![]() 另一個焦點是
另一個焦點是![]() ,且
,且![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)直線![]() 過點
過點![]() ,且與橢圓
,且與橢圓![]() 交于
交于![]() 兩點,求
兩點,求![]() 的內切圓面積的最大值.
的內切圓面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知下列命題:
①在線性回歸模型中,相關指數![]() 越接近于1,表示回歸效果越好;
越接近于1,表示回歸效果越好;
②兩個變量相關性越強,則相關系數r就越接近于1;
③在回歸直線方程![]() 中,當解釋變量
中,當解釋變量![]() 每增加一個單位時,預報變量
每增加一個單位時,預報變量![]() 平均減少0.5個單位;
平均減少0.5個單位;
④兩個模型中殘差平方和越小的模型擬合的效果越好.
⑤回歸直線![]() 恒過樣本點的中心
恒過樣本點的中心![]() ,且至少過一個樣本點;
,且至少過一個樣本點;
⑥若![]() 的觀測值滿足
的觀測值滿足![]() ≥6.635,我們有99%的把握認為吸煙與患肺病有關系,那么在100個吸煙的人中必有99人患有肺病;
≥6.635,我們有99%的把握認為吸煙與患肺病有關系,那么在100個吸煙的人中必有99人患有肺病;
⑦從統計量中得知有95%的把握認為吸煙與患肺病有關系,是指有5%的可能性使得推斷出現錯誤. 其中正確命題的序號是__________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com