
分析 若p∨q”為真,p∧q為假,則p,q一真一假,進而答案.
解答 解:對于P:$\left\{{\begin{array}{l}{△>0}\\{{x_1}+{x_2}<0}\\{{x_1}{x_2}>0}\end{array}}\right.$,則得k>4(2分)
對于q:把圓的方程化為標準方程得(x+$\frac{k}{2}$)2+(y+1)2=16-$\frac{3k2}{4}$
所以16-$\frac{3k2}{4}$>0,解得-$\frac{8\sqrt{3}}{3}$<k<$\frac{8\sqrt{3}}{3}$.
由題意知點(1,2)應(yīng)在已知圓的外部,
把點代入圓的方程得1+4+k+4+k2-15>0,
即(k-2)(k+3)>0,解得k>2或k<-3,
則實數(shù)k的取值范圍是-$\frac{8\sqrt{3}}{3}$<k<-3,或2<k<$\frac{8\sqrt{3}}{3}$.(7分)
若p∨q”為真,p∧q為假,則p,q一真一假
(1)p為真,q為假時,易得k∈(4,+∞).(9分)
(2)p為假,q為真時,易得$k∈(-\frac{8\sqrt{3}}{3},-3)∪(2,4]$(11分)
所以所求實數(shù)m的取值范圍是$k∈(-\frac{8\sqrt{3}}{3},-3)∪(2,+∞)$(12分)
點評 本題以命題的真假判斷與應(yīng)用為載體,考查了復(fù)合命題,方程根的個數(shù),直線與圓的位置關(guān)系等知識點,難度中檔.


 名校聯(lián)盟快樂課堂系列答案
名校聯(lián)盟快樂課堂系列答案科目:高中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:選擇題
| A. | 設(shè)p:f(x)=x3+2x2+mx+1是R上的單調(diào)增函數(shù),$q:m≥\frac{4}{3}$,則p是q的必要不充分條件 | |
| B. | 若命題$p:?{x_0}∈R,x_0^2-{x_0}+1≤0$,則¬p:?x∈R,x2-x+1>0 | |
| C. | 奇函數(shù)f(x)定義域為R,且f(x-1)=-f(x),那么f(8)=0 | |
| D. | 命題“若x2+y2=0,則x=y=0”的逆否命題為“若x,y中至少有一個不為0,則x2+y2≠0” |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
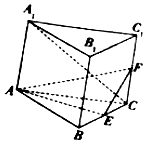 如圖直三棱柱ABC-A1B1C1的底面是邊長為4的正三角形,E、F分別是BC,CC1的中點,
如圖直三棱柱ABC-A1B1C1的底面是邊長為4的正三角形,E、F分別是BC,CC1的中點,查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com