
【題目】已知函數(shù)![]() (
(![]() ,
, ![]() 為自然對數(shù)的底數(shù)).
為自然對數(shù)的底數(shù)).
(1)討論函數(shù)![]() 的單調(diào)性;
的單調(diào)性;
(2)若![]() ,函數(shù)
,函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上為增函數(shù),求整數(shù)
上為增函數(shù),求整數(shù)![]() 的最大值.
的最大值.
【答案】(1)見解析;(2)![]() .
.
【解析】試題分析:(1)求出![]() ,令
,令![]() 求得
求得![]() 的范圍,可得函數(shù)
的范圍,可得函數(shù)![]() 增區(qū)間,
增區(qū)間, ![]() 求得
求得![]() 的范圍,可得函數(shù)
的范圍,可得函數(shù)![]() 的減區(qū)間;;(2)由于函數(shù)
的減區(qū)間;;(2)由于函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上為增函數(shù),則其導(dǎo)函數(shù)
上為增函數(shù),則其導(dǎo)函數(shù)![]() 在
在![]() 恒成立,再分離參數(shù)
恒成立,再分離參數(shù)![]() 得到
得到![]() 在
在![]() 恒成立,此時問題變?yōu)榍蠛瘮?shù)
恒成立,此時問題變?yōu)榍蠛瘮?shù)![]() 在區(qū)間
在區(qū)間![]() 上的最小值問題,利用導(dǎo)數(shù)研究其單調(diào)性,求出最小值即可得結(jié)果.
上的最小值問題,利用導(dǎo)數(shù)研究其單調(diào)性,求出最小值即可得結(jié)果.
試題解析:(1)由![]() 得
得![]()
當(dāng)![]() 時,
時, ![]() ,所以
,所以![]() 在
在![]() 上為增函數(shù);
上為增函數(shù);
當(dāng)![]() 時,
時, ![]() 時,
時, ![]() ,
, ![]() 時,
時, ![]() ,
,
所以![]() 在
在![]() 為減函數(shù),在
為減函數(shù),在![]() 為增函數(shù),
為增函數(shù),
(2)當(dāng)![]() 時,
時, ![]()
則![]()
若![]() 在區(qū)間
在區(qū)間![]() 上為增函數(shù),則
上為增函數(shù),則![]() 在
在![]() 上恒成立,即
上恒成立,即![]() 在
在![]() 上恒成立.
上恒成立.
令![]() ,
, ![]() ;則
;則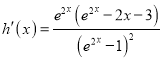 ,
, ![]() ;
;
令![]() ,則
,則![]()
當(dāng)![]() 時,
時, ![]() ,則
,則![]() 在
在![]() 單調(diào)遞增
單調(diào)遞增
而![]() ,
, ![]()
所以函數(shù)![]() 在
在![]() 只有一個零點,設(shè)為
只有一個零點,設(shè)為![]() ,
,
即![]() 時,
時, ![]() ,即
,即![]() ;
; ![]() 時,
時, ![]() ,即
,即![]() ,
,
∴![]() ,
, ![]() ,有最小值
,有最小值![]() ,
,
把![]() 代入上式可得
代入上式可得![]() ,
,
又因為![]() ,所以
,所以![]() ,
,
又![]() 恒成立,所以
恒成立,所以![]() ,又因為
,又因為![]() 為整數(shù),所以
為整數(shù),所以![]() ,
,
所以整數(shù)![]() 的最大值為
的最大值為![]() .
.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】“荊、荊、襄、宜七校聯(lián)考”正在如期開展,組委會為了解各所學(xué)校學(xué)生的學(xué)情,欲從四地選取200人作樣本開展調(diào)研.若來自荊州地區(qū)的考生有1000人,荊門地區(qū)的考生有2000人,襄陽地區(qū)的考生有3000人,宜昌地區(qū)的考生有2000人.為保證調(diào)研結(jié)果相對準(zhǔn)確,下列判斷正確的有( )
①用分層抽樣的方法分別抽取荊州地區(qū)學(xué)生25人、荊門地區(qū)學(xué)生50人、襄陽地區(qū)學(xué)生75人、宜昌地區(qū)學(xué)生50人;
②可采用簡單隨機抽樣的方法從所有考生中選出200人開展調(diào)研;
③宜昌地區(qū)學(xué)生小劉被選中的概率為![]() ;
;
④襄陽地區(qū)學(xué)生小張被選中的概率為![]() .
.
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】總體由編號為01,02,03,![]() ,49,50的50個個體組成,利用隨機數(shù)表(以下選取了隨機數(shù)表中的第1行和第2行)選取5個個體,選取方法是從隨機數(shù)表第1行的第9列和第10列數(shù)字開始由左向右讀取,則選出來的第4個個體的編號為( )
,49,50的50個個體組成,利用隨機數(shù)表(以下選取了隨機數(shù)表中的第1行和第2行)選取5個個體,選取方法是從隨機數(shù)表第1行的第9列和第10列數(shù)字開始由左向右讀取,則選出來的第4個個體的編號為( )
78 16 65 72 08 02 63 14 07 02 43 69 69 38 74 |
32 04 94 23 49 55 80 20 36 35 48 69 97 28 01 |
A. 05 B. 09 C. 07 D. 20
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知拋物線![]() ,直線
,直線![]() 與E交于A、B兩點,且
與E交于A、B兩點,且![]() ,其中O為原點.
,其中O為原點.
(1)求拋物線E的方程;
(2)點C坐標(biāo)為![]() ,記直線CA、CB的斜率分別為
,記直線CA、CB的斜率分別為![]() ,證明:
,證明: ![]() 為定值.
為定值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】(本小題滿分12分)已知橢圓![]()
![]() (
(![]() )的半焦距為
)的半焦距為![]() ,原點
,原點![]() 到經(jīng)過兩點
到經(jīng)過兩點![]() ,
,![]() 的直線的距離為
的直線的距離為![]() .
.
(Ⅰ)求橢圓![]() 的離心率;
的離心率;
(Ⅱ)如圖,![]() 是圓
是圓![]()
![]() 的一條直徑,若橢圓
的一條直徑,若橢圓![]() 經(jīng)過
經(jīng)過![]() ,
,![]() 兩點,求橢圓
兩點,求橢圓![]() 的方程.
的方程.

查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知![]() 為函數(shù)
為函數(shù)![]() 的導(dǎo)函數(shù),且
的導(dǎo)函數(shù),且![]() .
.
(1)判斷函數(shù)![]() 的單調(diào)性;
的單調(diào)性;
(2)若![]() ,討論函數(shù)
,討論函數(shù)![]() 零點的個數(shù).
零點的個數(shù).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】一座圓拱橋,當(dāng)水面在如圖所示位置時,拱頂離水面2米,水面寬12米,當(dāng)水面下降1米后,水面寬多少米?
![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() :
:![]()
![]() 的一個焦點與拋物線
的一個焦點與拋物線![]() 的焦點重合,且過點
的焦點重合,且過點![]() .過點
.過點![]() 的直線
的直線![]() 交橢圓
交橢圓![]() 于
于![]() ,
, ![]() 兩點,
兩點, ![]() 為橢圓的左頂點.
為橢圓的左頂點.
(Ⅰ)求橢圓![]() 的標(biāo)準(zhǔn)方程;
的標(biāo)準(zhǔn)方程;
(Ⅱ)求![]() 面積的最大值,并求此時直線
面積的最大值,并求此時直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】對某校高三年級學(xué)生參加社區(qū)服務(wù)次數(shù)進(jìn)行統(tǒng)計,隨機抽取M名學(xué)生作為樣本,得到這M名學(xué)生參加社區(qū)服務(wù)的次數(shù).根據(jù)此數(shù)據(jù)作出了頻數(shù)與頻率的統(tǒng)計表如下,頻率分布直方圖如圖:
分組 | 頻數(shù) | 頻率 |
[10,15) | 10 | 0.25 |
[15,20) | 24 | n |
[20,25) | m | p |
[25,30) | 2 | 0.05 |
合計 | M | 1 |

(1)求出表中M,p及圖中a的值;
(2)若該校高三學(xué)生有240人,試估計該校高三學(xué)生參加社區(qū)服務(wù)的次數(shù)在區(qū)間[10,15)內(nèi)的人數(shù);
(3)在所取樣本中,從參加社區(qū)服務(wù)的次數(shù)不少于20次的學(xué)生中任選2人,求至多一人參加社區(qū)服務(wù)次數(shù)在區(qū)間[25,30)內(nèi)的概率.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com