
一邊長為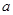 的正方形鐵片,鐵片的四角截去四個邊長均為
的正方形鐵片,鐵片的四角截去四個邊長均為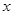 的小正方形,然后做成一個無蓋方盒。
的小正方形,然后做成一個無蓋方盒。
(1)試把方盒的容積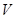 表示為
表示為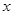 的函數;
的函數;
(2)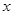 多大時,方盒的容積
多大時,方盒的容積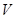 最大?
最大?
科目:高中數學 來源:2014屆廣東省佛山市高二下學期期中考試文科數學試卷(解析版) 題型:解答題
一邊長為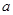 的正方形鐵片,鐵片的四角截去四個邊長均為
的正方形鐵片,鐵片的四角截去四個邊長均為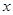 的小正方形,然后做成一個無蓋方盒。
的小正方形,然后做成一個無蓋方盒。
(1)試把方盒的容積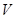 表示為
表示為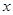 的函數;(2)
的函數;(2)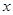 多大時,方盒的容積
多大時,方盒的容積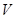 最大?
最大?
查看答案和解析>>
科目:高中數學 來源:2013屆福建省高二下學期期末考試理科數學試卷(解析版) 題型:解答題
有一邊長為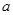 的正方形鐵片,鐵片的四角截去四個邊長為
的正方形鐵片,鐵片的四角截去四個邊長為 的小正方形,然后做成一個無蓋方盒。
的小正方形,然后做成一個無蓋方盒。
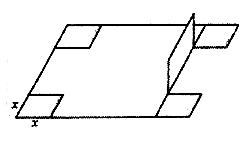
(1)試把方盒的容積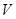 表示成
表示成 的函數;
的函數;
(2)求 多大時,做成方盒的容積
多大時,做成方盒的容積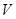 最大。
最大。
查看答案和解析>>
科目:高中數學 來源:2010-2011學年廣東省增城市高三畢業班調研測試數學理卷 題型:解答題
(本題滿分13分)一邊長為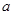 的正方形鐵片,鐵片的四角截去四個邊長均為
的正方形鐵片,鐵片的四角截去四個邊長均為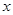 的小正方形,然后做成一個無蓋方盒.
的小正方形,然后做成一個無蓋方盒.
(1)將方盒的容積表示成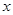 的函數
的函數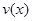 ;
;
(2)當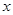 是多少時,方盒的容積最大?最大容積是多少?
是多少時,方盒的容積最大?最大容積是多少?
查看答案和解析>>
科目:高中數學 來源:2013屆安徽省宿州市高二下學期期中質量檢測理科數學試卷(解析版) 題型:解答題
一邊長為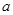 的正方形鐵片,鐵片的四角各截去一個邊長為
的正方形鐵片,鐵片的四角各截去一個邊長為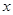 的小正方形,然后做成一個無蓋方盒.
的小正方形,然后做成一個無蓋方盒.
(Ⅰ)試把方盒的體積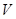 表示為
表示為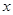 的函數;
的函數;
(Ⅱ)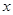 多大時,方盒的體積
多大時,方盒的體積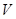 最大?
最大?
【解析】本試題主要考查了函數在實際生活中表示體積的最值的運用。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com