【題目】三國時代吳國數(shù)學家趙爽所注《周髀算經(jīng)》中給出了勾股定理的絕妙證明.下面是趙爽的弦圖及注文，弦圖是一個以勾股形之弦為邊的正方形，其面積稱為弦實.圖中包含四個全等的勾股形及一個小正方形，分別涂成紅（朱）色及黃色，其面積稱為朱實、黃實，利用
，化簡，得
.設勾股形中勾股比為
，若向弦圖內(nèi)隨機拋擲
顆圖釘（大小忽略不計），則落在黃色圖形內(nèi)的圖釘數(shù)大約為（ ）
A. 
B. 
C. 
D. 
科目：高中數(shù)學 來源： 題型：
【題目】已知橢圓
的左、右焦點
，
，
是橢圓
上的動點，且
面積的最大值為
.
（1）求橢圓的方程及離心率；
（2）若
是橢圓的左、右頂點，直線
與橢圓在點
處的切線交于點
，當點在橢圓上運動時，求證：以
為直徑的圓與直線
恒相切.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】在平面直角坐標系
，
．以坐標原點為極點，
軸正半軸為極軸建立極坐標系，已知曲線
的極坐標方程為
，點
為上的動點，
為
的中點．
（1）請求出點軌跡
的直角坐標方程；
（2）設點
的極坐標為
若直線
經(jīng)過點且與曲線交于點
，弦
的中點為
，求
的取值范圍．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知橢圓
：
的兩個焦點為
,
,焦距為
,直線
:
與橢圓相交于
,
兩點,
為弦
的中點.
（1）求橢圓的標準方程;
（2）若直線:
與橢圓相交于不同的兩點
,
,
,若
（
為坐標原點）,求
的取值范圍.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】秦九韶是我國南宋時期的數(shù)學家，普州（現(xiàn)四川省安岳縣）人，他在所著的《數(shù)書九章》中提出的多項式求值的秦九韶算法，至今仍是比較先進的算法.如圖所示的程序框圖給出了利用秦九韶算法求某多項式值的一個實例，若輸入
，
的值分別為5，2，則輸出
的值為（ ）
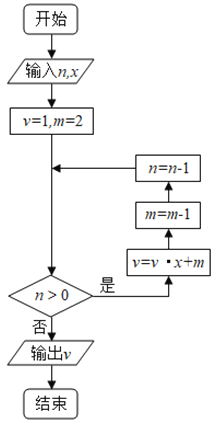
A.64B.68C.72D.133
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】學校藝術節(jié)對
四件參賽作品只評一件一等獎，在評獎揭曉前，甲，乙，丙，丁四位同學對這四件參賽作品預測如下：
甲說：“是
或
作品獲得一等獎”； 乙說：“ 
作品獲得一等獎”；
丙說：“ 
兩件作品未獲得一等獎”； 丁說：“是作品獲得一等獎”．
評獎揭曉后，發(fā)現(xiàn)這四位同學中只有兩位說的話是對的，則獲得一等獎的作品是_________．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】十二生肖是十二地支的形象化代表，即子（鼠）、丑（牛）、寅（虎）、卯（兔）、辰（龍）、巳（蛇）、午（馬）、未（羊）、申（猴）、酉（雞）、戌（狗）、亥（豬），每一個人的出生年份對應了十二種動物中的一種，即自己的屬相.現(xiàn)有印著六種不同生肖圖案（包含馬、羊）的毛絨娃娃各一個，小張同學的屬相為馬，小李同學的屬相為羊，現(xiàn)在這兩位同學從這六個毛絨娃娃中各隨機取一個（不放回），則這兩位同學都拿到自己屬相的毛絨娃娃的概率是（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知
為坐標原點，點
和點
，動點
滿足：
.
（1）求動點的軌跡曲線
的方程并說明是何種曲線；
（2）若拋物線
：
的焦點
恰為曲線的頂點，過點的直線
與拋物線交于
，
兩點，
，求直線的方程.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
