
【題目】已知函數![]() ,
,![]() .
.
(1)若直線![]() 與函數
與函數![]() 的圖象相切,求實數
的圖象相切,求實數![]() 的值;
的值;
(2)若存在![]() ,
,![]() ,使
,使![]() ,且
,且![]() ,求實數
,求實數![]() 的取值范圍;
的取值范圍;
(3)當![]() 時,求證:
時,求證:![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)詳見解析.
;(3)詳見解析.
【解析】
(1)由f′(x0)![]() .可得切線方程為:y=(
.可得切線方程為:y=(![]() )x+lnx0,與直線y=2x完全相同,可得
)x+lnx0,與直線y=2x完全相同,可得![]() =2,lnx0=0.即可得出a.
=2,lnx0=0.即可得出a.
(2)設t(x)=ex﹣x,x∈R.t′(x)=ex﹣1,利用導數研究其單調性可得0是函數t(x)的極小值點,可得![]() .再由g(x2)=0,解得x2,可得x1的范圍.從而問題可轉化為函數f(x)=lnx﹣ax+1在x∈(1,+∞)上有零點.由f′(x)
.再由g(x2)=0,解得x2,可得x1的范圍.從而問題可轉化為函數f(x)=lnx﹣ax+1在x∈(1,+∞)上有零點.由f′(x)![]() a
a![]() .對a分類討論,研究其單調性即可得出.
.對a分類討論,研究其單調性即可得出.
(3)構造函數F(x)=x2+g(x)﹣f(x),利用導數研究其單調性極值與最值即可得出.
(1)設切點坐標為![]() ,
,
由![]() ,得
,得![]() ,
,
所以切線方程為:![]() ,
,
即![]() .
.
因為直線![]() 與函數
與函數![]() 的圖象相切,
的圖象相切,
所以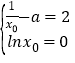 ,解得
,解得![]() .
.
(2)設![]() ,則
,則![]() ,令
,令![]() ,得
,得![]() ,
,
且當![]() 時,
時,![]() :當
:當![]() 時,
時,![]() ,
,
所以![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增,
上單調遞增,
所以![]() 在
在![]() 時取得極小值為0,即
時取得極小值為0,即![]() .
.
由![]() ,可得
,可得![]() ,
,
所以![]() 即為
即為![]() ,
,
由題意可得:函數![]() 在
在![]() 上有零點.
上有零點.
因為![]() ,
,
當![]() 時,
時,![]() ,函數
,函數![]() 在
在![]() 上單調遞增,
上單調遞增,
所以![]() ,函數
,函數![]() 在
在![]() 上無零點:
上無零點:
當![]() 時,令
時,令![]() ,得
,得![]() .
.
①若![]() ,即
,即![]() 時,
時,![]() 在
在![]() 上恒成立,
上恒成立,
所以函數![]() 在
在![]() 上單調遞減,
上單調遞減,
所以![]() ,函數
,函數![]() 在
在![]() 上無零點:
上無零點:
②若![]() ,即
,即![]() 時,
時,
當![]() 時,
時,![]() :當
:當![]() 時,
時,![]() .
.
所以函數![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減,
上單調遞減,
所以![]() ,
,
因為![]() ,所以函數
,所以函數![]() 在
在![]() 上無零點:
上無零點:
又![]() ,
,
令![]() ,
,
則![]() 在
在![]() 上恒成立,
上恒成立,
所以![]() 在
在![]() 上單調遞增,
上單調遞增,
所以![]() ,即
,即![]() ,
,
所以![]() ,且
,且![]() 在
在![]() 的圖象連續不斷,
的圖象連續不斷,
所以函數![]() 在
在![]() 上有且只有一個零點,
上有且只有一個零點,
即函數![]() 在
在![]() 上有零點.
上有零點.
綜上所述,![]() .
.
(3)當![]() 時,
時,![]() ,
,
令![]()
![]() ,
,
則![]() ,
,
令![]() ,則當
,則當![]() 時,
時,![]() ,
,
所以函數![]() 在區間
在區間![]() 上是增函數,
上是增函數,
又![]() ,
,![]() ,
,
所以函數![]() 存在唯一的零點
存在唯一的零點![]() ,
,
且當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() .
.
所以當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() .
.
所以函數![]() 在
在![]() 上遞減,在
上遞減,在![]() 上遞增,
上遞增,
故![]() ,
,
由![]() 得:
得:![]() ,
,
兩邊取對數得:![]() ,故
,故![]() ,
,
所以![]() ,即
,即![]() .
.


 中考利劍中考試卷匯編系列答案
中考利劍中考試卷匯編系列答案 教育世家狀元卷系列答案
教育世家狀元卷系列答案 黃岡課堂作業本系列答案
黃岡課堂作業本系列答案 單元加期末復習先鋒大考卷系列答案
單元加期末復習先鋒大考卷系列答案科目:高中數學 來源: 題型:
【題目】過直線2x+y+4=0和圓x2+y2+2x﹣4y+1=0的交點,且面積最小的圓方程為( )
A.(x+![]() )2+(y+
)2+(y+![]() )2=
)2=![]() B.(x﹣
B.(x﹣![]() )2+(y﹣
)2+(y﹣![]() )2=
)2=![]()
C.(x﹣![]() )2+(y+
)2+(y+![]() )2=
)2=![]() D.(x+
D.(x+![]() )2+(y﹣
)2+(y﹣![]() )2=
)2=![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C:![]() (a>b>0)的左.右頂點分別為A,B,離心率為
(a>b>0)的左.右頂點分別為A,B,離心率為![]() ,點P
,點P![]() 為橢圓上一點.
為橢圓上一點.
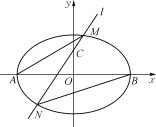
(1) 求橢圓C的標準方程;
(2) 如圖,過點C(0,1)且斜率大于1的直線l與橢圓交于M,N兩點,記直線AM的斜率為k1,直線BN的斜率為k2,若k1=2k2,求直線l斜率的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,點
中,點![]() 是圓
是圓![]() :
:![]() 上的動點,定點
上的動點,定點![]() ,線段
,線段![]() 的垂直平分線交
的垂直平分線交![]() 于
于![]() ,記
,記![]() 點的軌跡為
點的軌跡為![]() .
.
(Ⅰ)求軌跡![]() 的方程;
的方程;
(Ⅱ)若動直線![]() :
:![]() 與軌跡
與軌跡![]() 交于不同的兩點
交于不同的兩點![]() 、
、![]() ,點
,點![]() 在軌跡
在軌跡![]() 上,且四邊形
上,且四邊形![]() 為平行四邊形.證明:四邊形
為平行四邊形.證明:四邊形![]() 的面積為定值.
的面積為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
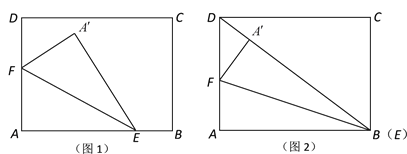
【題目】南通風箏是江蘇傳統手工藝品之一.現用一張長2 m,寬1.5 m的長方形牛皮紙ABCD裁剪風箏面,裁剪方法如下:分別在邊AB,AD上取點E,F,將三角形AEF沿直線EF翻折到![]() 處,點
處,點![]() 落在牛皮紙上,沿
落在牛皮紙上,沿![]() ,
,![]() 裁剪并展開,得到風箏面
裁剪并展開,得到風箏面![]() ,如圖1.
,如圖1.
(1)若點E恰好與點B重合,且點![]() 在BD上,如圖2,求風箏面
在BD上,如圖2,求風箏面![]() 的面積;
的面積;
(2)當風箏面![]() 的面積為
的面積為![]() 時,求點
時,求點![]() 到AB距離的最大值.
到AB距離的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某大學生參加社會實踐活動,對某公司1月份至6月份銷售某種配件的銷售量及銷售單價進行了調查,銷售單價![]() 和銷售量
和銷售量![]() 之間的一組數據如下表所示:
之間的一組數據如下表所示:
月份 | 1 | 2 | 3 | 4 | 5 | 6 |
銷售單價 | 9 | 9.5 | 10 | 10.5 | 11 | 8 |
銷售量 | 11 | 10 | 8 | 6 | 5 | 14.2 |
(1)根據1至5月份的數據,先求出![]() 關于
關于![]() 的回歸直線方程;6月份的數據作為檢驗數據.若由回歸直線方程得到的預測數據與檢驗數據的誤差不超過
的回歸直線方程;6月份的數據作為檢驗數據.若由回歸直線方程得到的預測數據與檢驗數據的誤差不超過![]() ,則認為所得到的回歸直線方程是理想的.試問所求得的回歸直線方程是否理想?
,則認為所得到的回歸直線方程是理想的.試問所求得的回歸直線方程是否理想?
(2)預計在今后的銷售中,銷售量與銷售單價仍然服從(1)中的回歸關系,如果該種機器配件的成本是![]() 元/件,那么該配件的銷售單價應定為多少元才能獲得最大利潤?(注:利潤=銷售收入-成本).
元/件,那么該配件的銷售單價應定為多少元才能獲得最大利潤?(注:利潤=銷售收入-成本).
參考數據:![]() ,
,![]() .
.
參考公式:對于一組數據![]() ,
,![]() ,…,
,…,![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為:
的斜率和截距的最小二乘估計分別為: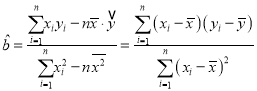 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓心在![]() 軸上的圓
軸上的圓![]() 與直線
與直線![]() 切于點
切于點![]() .
.
(1)求圓![]() 的標準方程;
的標準方程;
(2)已知![]() ,經過原點,且斜率為正數的直線
,經過原點,且斜率為正數的直線![]() 與圓
與圓![]() 交于
交于![]() 兩點.
兩點.
(ⅰ)求證: ![]() 為定值;
為定值;
(ⅱ)求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地區某農產品近幾年的產量統計如下表:

(1)根據表中數據,建立![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(2)若近幾年該農產品每千克的價格![]() (單位:元)與年產量
(單位:元)與年產量![]() 滿足的函數關系式為
滿足的函數關系式為![]() ,且每年該農產品都能售完.
,且每年該農產品都能售完.
①根據(1)中所建立的回歸方程預測該地區![]() 年該農產品的產量;
年該農產品的產量;
②當![]() 為何值時,銷售額
為何值時,銷售額![]() 最大?
最大?
附:對于一組數據![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為:
的斜率和截距的最小二乘估計分別為: 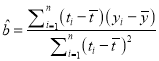 ,
, ![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com