
已知曲線 的極坐標(biāo)方程為
的極坐標(biāo)方程為 ,以極點為原點,極軸為
,以極點為原點,極軸為 軸的正半軸建立平面直角坐標(biāo)系,設(shè)直線
軸的正半軸建立平面直角坐標(biāo)系,設(shè)直線 的參數(shù)方程為
的參數(shù)方程為 (
( 為參數(shù)).
為參數(shù)).
(1)求曲線 的直角坐標(biāo)方程與直線
的直角坐標(biāo)方程與直線 的普通方程;
的普通方程;
(2)設(shè)曲線 與直線
與直線 相交于
相交于 兩點,以
兩點,以 為一條邊作曲線
為一條邊作曲線 的內(nèi)接矩形,求該矩形的面積.
的內(nèi)接矩形,求該矩形的面積.
(1)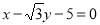 ;(2)
;(2)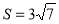
【解析】
試題分析:(1)將參數(shù)方程轉(zhuǎn)化為直角坐標(biāo)系下的普通方程,需要根據(jù)參數(shù)方程的結(jié)構(gòu)特征,選取恰當(dāng)?shù)南麉⒎椒ǎR姷南麉⒎椒ㄓ校捍胂麉⒎ā⒓訙p消參法、平方消參法;(2)將參數(shù)方程轉(zhuǎn)化為普通方程時,要注意兩種方程的等價性,不要增解、漏解,若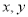 有范圍限制,要標(biāo)出
有范圍限制,要標(biāo)出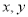 的取值范圍;(3)點到直線的距離公式,圓的弦長的常用求法:(1)幾何法:求圓的半徑
的取值范圍;(3)點到直線的距離公式,圓的弦長的常用求法:(1)幾何法:求圓的半徑 ,弦心距
,弦心距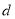 ,弦長
,弦長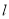 ,則
,則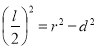 (2)代數(shù)方法:運用根與系數(shù)的關(guān)系及弦長公式
(2)代數(shù)方法:運用根與系數(shù)的關(guān)系及弦長公式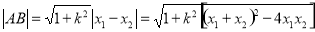 .
.
試題解析:【解析】
(1)對于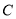 :由
:由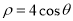 ,得
,得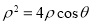 ,進而
,進而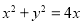 . 2分
. 2分
對于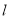 :由
:由 (
(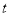 為參數(shù)),得
為參數(shù)),得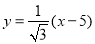 ,即
,即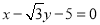 . 4分
. 4分
(2)由(1)可知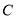 為圓,圓心為
為圓,圓心為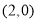 ,半徑為2,弦心距
,半徑為2,弦心距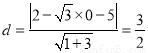 , 6分.弦長
, 6分.弦長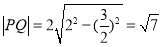 , 8分.
, 8分.
因此以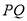 為邊的圓
為邊的圓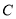 的內(nèi)接矩形面積
的內(nèi)接矩形面積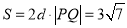 10分
10分
考點:1、參數(shù)方程與普通方程的互化;2、求矩形的面積.


 舉一反三同步巧講精練系列答案
舉一反三同步巧講精練系列答案 口算與應(yīng)用題卡系列答案
口算與應(yīng)用題卡系列答案 名師點睛字詞句段篇系列答案
名師點睛字詞句段篇系列答案科目:高中數(shù)學(xué) 來源:2013-2014學(xué)年福建省龍巖市高三上學(xué)期期末考試理科數(shù)學(xué)試卷(解析版) 題型:解答題
為了保障幼兒園兒童的人身安全,國家計劃在甲、乙兩省試行政府規(guī)范購置校車方案,計劃若干時間內(nèi)(以月為單位)在兩省共新購1000輛校車.其中甲省采取的新購方案是:本月新購校車10輛,以后每月的新購量比上一月增加50%;乙省采取的新購方案是:本月新購校車40輛,計劃以后每月比上一月多新購m輛.
(1)求經(jīng)過n個月,兩省新購校車的總數(shù)S(n);
(2)若兩省計劃在3個月內(nèi)完成新購目標(biāo),求m的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2015屆內(nèi)蒙古巴彥淖爾市高三10月月考理科數(shù)學(xué)試卷(解析版) 題型:選擇題
曲線 在點(-1,-3)處的切線方程是( )
在點(-1,-3)處的切線方程是( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2015屆內(nèi)蒙古巴彥淖爾市高三10月月考文科數(shù)學(xué)試卷(解析版) 題型:選擇題
已知函數(shù) 的零點分別是
的零點分別是 ,則
,則 的大小關(guān)系是( )
的大小關(guān)系是( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2015屆內(nèi)蒙古巴彥淖爾市高三10月月考文科數(shù)學(xué)試卷(解析版) 題型:選擇題
曲線 在點(-1,-3)處的切線方程是( )
在點(-1,-3)處的切線方程是( )
A . B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2015屆云南省高三上學(xué)期第一次月考理科數(shù)學(xué)試卷(解析版) 題型:解答題
在△ 中,角
中,角 的對邊分別為
的對邊分別為 .已知
.已知 ,
, ,且
,且
(1)求角 的大小;(2)求△
的大小;(2)求△ 的面積.
的面積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2015屆云南省高三上學(xué)期第一次月考理科數(shù)學(xué)試卷(解析版) 題型:選擇題
設(shè)變量 滿足
滿足 ,若目標(biāo)函數(shù)
,若目標(biāo)函數(shù) 的最小值為
的最小值為 ,則
,則 的值為( )
的值為( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2015屆云南省高三上學(xué)期第一次月考文科數(shù)學(xué)試卷(解析版) 題型:填空題
已知等差數(shù)列 中,
中, ,那么
,那么 .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2015屆云南省等校高三12月份統(tǒng)一考試文科數(shù)學(xué)試卷(解析版) 題型:選擇題
從個位數(shù)與十位數(shù)之和為奇數(shù)的兩位數(shù)中任取一個,其中個位數(shù)為0的概率是( )
A.  B.
B. C.
C. D.
D.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com