
【題目】已知數列![]() 滿足
滿足![]() ,
,![]() ,
,![]() .
.
(1)若![]() ,
,![]() ,
,![]() ,求
,求![]() 的取值范圍;
的取值范圍;
(2)若![]() 是公比為
是公比為![]() 的等比數列,
的等比數列,![]() ,
,![]() ,
,![]() ,求
,求![]() 的取值范圍;
的取值范圍;
(3)若![]() 成等差數列,且
成等差數列,且![]() ,求正整數
,求正整數![]() 的最大值.
的最大值.
【答案】(1)![]() ,(2)
,(2)![]() ,(3)
,(3)![]()
【解析】
(1)由題意得![]() ,又
,又![]() ,將已知代入可求出
,將已知代入可求出![]() 的范圍;
的范圍;
(2)先求出通項![]() ,由
,由![]() 求出
求出![]() ,對
,對![]() 分類討論求出
分類討論求出![]() ,分別代入不等式
,分別代入不等式![]() ,得到關于
,得到關于![]() 的不等式組,解不等式組求出
的不等式組,解不等式組求出![]() 的范圍;
的范圍;
(3)由題意得到關于![]() 的不等式,得出
的不等式,得出![]() 的最大值,并得出
的最大值,并得出![]() 取最大值時
取最大值時![]() 的公差
的公差
解:(1)由題意得,![]() ,所以
,所以![]() ,
,
又因為![]() ,所以
,所以![]() ,得
,得![]() ,
,
綜上所述,![]()
(2)由已知得,![]() ,
,![]()
所以![]() ,
,
當![]() 時,
時,![]() ,
,![]() ,即
,即![]() ,成立,
,成立,
當![]() 時,
時,![]() ,
,![]() ,即
,即![]() ,
,
![]() ,得
,得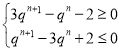 ,
,
因為![]() ,故
,故![]() ,
,
對于不等式![]() ,令
,令![]() ,得
,得![]() ,
,
解得![]() ,
,
又當![]() ,
,![]() ,
,
所以![]() 成立
成立
所以![]() ,
,
當![]() 時,
時,![]() ,
,![]() ,
,
即![]() ,
,
所以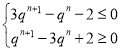 ,
,
因為![]() ,
,
所以![]() ,
,
![]() ,
,
所以當![]() 時,不等式恒成立,
時,不等式恒成立,
綜上所述,![]() 的取值范圍為
的取值范圍為![]()
(3)設![]() 的公差為
的公差為![]() ,由
,由![]() ,且
,且![]() ,
,
得![]() ,
,
即![]() ,
,
當![]() 時,
時,![]() ,
,
當![]() 時,由
時,由![]() ,得
,得![]() ,
,
所以![]() ,
,
所以![]() ,
,
即![]() ,得
,得![]() ,
,
所以![]() 的最大值為
的最大值為![]()


 芝麻開花課程新體驗系列答案
芝麻開花課程新體驗系列答案 怎樣學好牛津英語系列答案
怎樣學好牛津英語系列答案科目:高中數學 來源: 題型:
【題目】20名學生某次數學考試成績(單位:分)的頻率分布直方圖如圖.

(1)求頻率分布直方圖中a的值;
(2)估計總體中成績落在[50,60)中的學生人數;
(3)根據頻率分布直方圖估計20名學生數學考試成績的眾數,平均數;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() ,圓
,圓![]() 內一定點
內一定點![]() ,動圓
,動圓![]() 過點
過點![]() 且與圓
且與圓![]() 內切.記動圓圓心
內切.記動圓圓心![]() 的軌跡為
的軌跡為![]() .
.
(Ⅰ)求軌跡![]() 方程;
方程;
(II)過點![]() 的動直線l交軌跡
的動直線l交軌跡![]() 于M,N兩點,試問:在坐標平面上是否存在一個定點Q,使得以線段MN為直徑的圓恒過點Q?若存在,求出點Q的坐標;若不存在,請說明理由.
于M,N兩點,試問:在坐標平面上是否存在一個定點Q,使得以線段MN為直徑的圓恒過點Q?若存在,求出點Q的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在△ABC中,已知CA=1,CB=2,∠ACB=60°.

(1)求|![]() |;
|;
(2)已知點D是AB上一點,滿足![]() =λ
=λ![]() ,點E是邊CB上一點,滿足
,點E是邊CB上一點,滿足![]() =λ
=λ![]() .
.
①當λ=![]() 時,求
時,求![]()
![]() ;
;
②是否存在非零實數λ,使得![]() ⊥
⊥![]() ?若存在,求出的λ值;若不存在,請說明理由.
?若存在,求出的λ值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列五個判斷:
①某校高二一班和高二二班的人數分別是m,n,某次測試數學平均分分別為a,b,則這兩個班的數學平均分為![]() ;
;
②10名工人生產同一種零件,生產的件數分別是15,17,14,10,15,17,17,16,14,12,設其平均數為a,中位數為b,眾數為c,則有c>a>b;
③設m![]() ,命題“若a>b,則
,命題“若a>b,則![]() ”的逆否命題為假命題;
”的逆否命題為假命題;
④命題p“方程![]() 表示橢圓”,命題q“
表示橢圓”,命題q“![]() 的取值范圍為1<
的取值范圍為1<![]() <4”,則p是q的充要條件;
<4”,則p是q的充要條件;
⑤線性相關系數r越大,兩個變量的線性相關性越強;反之,線性相關性越弱;
其中正確的個數有( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】【2018屆河南省南陽市第一中學高三上學期第八次考試】2017年5月14日至15日,“一帶一路”國際合作高峰論壇在中國首都北京舉行,會議期間,達成了多項國際合作協議.假設甲、乙兩種品牌的同類產品出口某國家的市場銷售量相等,該國質量檢驗部門為了解他們的使用壽命,現從這兩種品牌的產品中分別隨機抽取300個進行測試,結果統計如下圖所示.
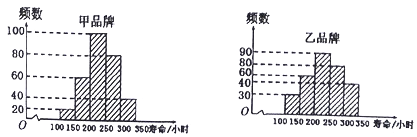
(1)估計甲品牌產品壽命小于200小時的概率;
(2)在抽取的這兩種品牌產品中,抽取壽命超過300小時的產品3個,設隨機變量![]() 表示抽取的產品是甲品牌的產品個數,求
表示抽取的產品是甲品牌的產品個數,求![]() 的分布列和數學期望值.
的分布列和數學期望值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,定長為3的線段
中,定長為3的線段![]() 兩端點
兩端點![]() 、
、![]() 分別在
分別在![]() 軸,
軸,![]() 軸上滑動,
軸上滑動,![]() 在線段
在線段![]() 上,且
上,且![]() .
.
(1)求點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)設點![]() 是軌跡
是軌跡![]() 上一點,從原點
上一點,從原點![]() 向圓
向圓![]() 作兩條切線分別與軌跡
作兩條切線分別與軌跡![]() 交于點
交于點![]() ,
,![]() ,直線
,直線![]() ,
,![]() 的斜率分別記為
的斜率分別記為![]() ,
,![]() .
.
①求證:![]() ;
;
②求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com