已知
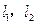
是過點
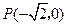
的兩條互相垂直的直線,且
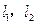
與雙曲線
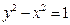
各兩個交點,分別為
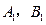
和
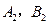
.
(1)求
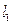
的斜率
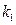
的取值范圍; (2)若
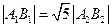
,求
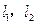
的方程.
(1)依題設,
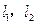
的斜率都存在,因為
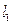
過點
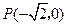
且與雙曲線有兩具交點,故方程組
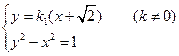
①
有兩組不同實根,在方程①中消去
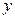
,整理得
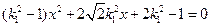
②
若
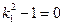
,則方程組①只有一個解,即
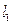
與雙曲線只有一個交點,與題設矛盾.故
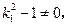
即
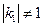
.方程②的判別式為
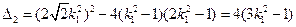
.
設
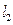
的斜率為
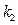
,因為
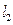
過點
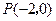
且與雙曲線有兩個交點,故方程組

③
有兩個不同的解.在方程組③中消去
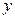
,整理得
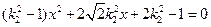
④
類似前面的討論,有
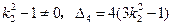
.
因為
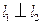
,所以
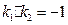
,于是,
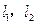
與雙曲線各有兩個交點,等價于下列混合組成立
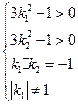
,解得
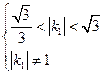
.
故
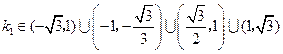
.
(2)設
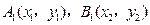
,則(1)的解答中方程②知
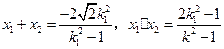
所以
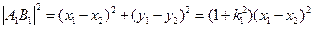
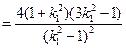
⑤
同理可得

⑥
由
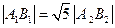
,得
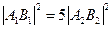
.
將⑤,⑥代入上式得
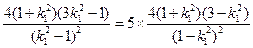
,
解得
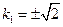
.
取
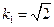
時,
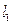
:
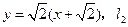
:
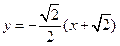
;
即
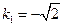
時,
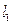
:
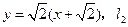
:
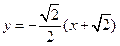
.
練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:解答題
已知雙曲線方程為
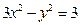
,以定點
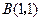
為中點的弦存在嗎?若存在,求出其所在直線的方程,若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
設點
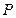
到
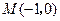
,
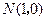
距離之差為
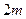
,到
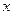
軸,
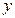
軸距離之比為
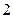
,求
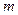
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
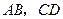
的半徑為
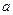
的定圓
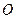
的兩互相垂直的直徑,作動弦
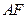
交
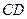
于
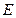
,引
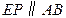
,且交
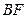
于
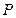
,求點
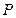
的軌跡方程.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
已知雙曲線
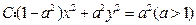
,若
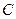
的上支頂點為
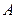
,且上支與直線
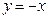
交于點
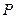
,以
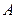
為焦點,
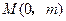
為頂點,開口向下的拋物線通過點
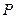
,當
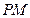
的斜率
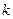
在區(qū)間
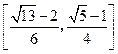
上變化時,求實數(shù)
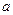
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
曲線
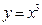
在
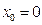
處的切線是否存在,若存在,求出切線的斜率和切線方程;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
已知⊙Q:(x-1)2+y2=16,動⊙M過定點P(-1,0)且與⊙Q相切,則M點的軌跡方程是: 。
查看答案和解析>>

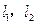 是過點
是過點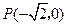 的兩條互相垂直的直線,且
的兩條互相垂直的直線,且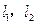 與雙曲線
與雙曲線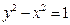 各兩個交點,分別為
各兩個交點,分別為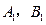 和
和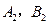 .
.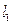 的斜率
的斜率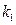 的取值范圍; (2)若
的取值范圍; (2)若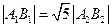 ,求
,求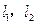 的方程.
的方程.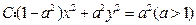 ,若
,若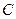 的上支頂點為
的上支頂點為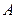 ,且上支與直線
,且上支與直線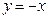 交于點
交于點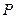 ,以
,以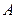 為焦點,
為焦點,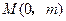 為頂點,開口向下的拋物線通過點
為頂點,開口向下的拋物線通過點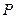 ,當
,當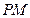 的斜率
的斜率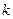 在區(qū)間
在區(qū)間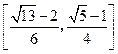 上變化時,求實數(shù)
上變化時,求實數(shù) 的取值范圍.
的取值范圍.