
【題目】某臍橙種植基地記錄了10棵臍橙樹在未使用新技術的年產量(單位:![]() )和使用了新技術后的年產量的數據變化,得到表格如下:
)和使用了新技術后的年產量的數據變化,得到表格如下:
未使用新技術的10棵臍橙樹的年產量
第一棵 | 第二棵 | 第三棵 | 第四棵 | 第五棵 | 第六棵 | 第七棵 | 第八棵 | 第九棵 | 第十棵 | |
年產量 | 30 | 32 | 30 | 40 | 40 | 35 | 36 | 45 | 42 | 30 |
使用了新技術后的10棵臍橙樹的年產量
第一棵 | 第二棵 | 第三棵 | 第四棵 | 第五棵 | 第六棵 | 第七棵 | 第八棵 | 第九棵 | 第十棵 | |
年產量 | 40 | 40 | 35 | 50 | 55 | 45 | 42 | 50 | 51 | 42 |
已知該基地共有20畝地,每畝地有50棵臍橙樹.
(1)估計該基地使用了新技術后,平均1棵臍橙樹的產量;
(2)估計該基地使用了新技術后,臍橙年總產量比未使用新技術將增產多少?
(3)由于受市場影響,導致使用新技術后臍橙的售價由原來(未使用新技術時)的每千克10元降為每千克9元,試估計該基地使用新技術后臍橙年總收入比原來增加的百分數.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】
(1)利用平均數的計算公式,得使用了新技術后的10棵臍橙樹的年產量的平均值,即可作出結論;
(2)求得未使用新技術的10棵臍橙樹的年產量的平均值,比較即可得出基地使用了新技術后,臍橙年總產量比未使用新技術將增產量.
(3)分別求得未使用新技術時的臍橙銷售總收入和使用了新技術后的臍橙銷售總收入,即可得到答案。
(1)使用了新技術后的10棵臍橙樹的年產量的平均值為
![]()
![]() ,
,
故可估計該基地使用了新技術后,平均1棵臍橙樹的產量為![]() .
.
(2)未使用新技術的10棵臍橙樹的年產量的平均值為
![]()
![]() ,
,
故估計該基地使用了新技術后,臍橙年總產量比未使用新技術將增產![]() .
.
(3)未使用新技術時的臍橙銷售總收入為![]() ,
,
使用了新技術后的臍橙銷售總收入為![]() ,
,
故估計該基地使用新技術后臍橙年總收入比原來增加的百分數為![]() .
.


科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左、右焦點為
的左、右焦點為![]() ,離心率為
,離心率為![]() ,點
,點![]() 在橢圓
在橢圓![]() 上,且
上,且![]() 的面積的最大值為
的面積的最大值為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)已知直線![]() 與橢圓
與橢圓![]() 交于不同的兩點
交于不同的兩點![]() ,若在
,若在![]() 軸上存在點
軸上存在點![]() ,使得
,使得![]() ,求實數
,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 的展開式中第5項與第7項的二項數系數相等,且展開式的各項系數之和為1024,則下列說法正確的是( )
的展開式中第5項與第7項的二項數系數相等,且展開式的各項系數之和為1024,則下列說法正確的是( )
A.展開式中奇數項的二項式系數和為256
B.展開式中第6項的系數最大
C.展開式中存在常數項
D.展開式中含![]() 項的系數為45
項的系數為45
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】體育測試成績分為四個等級:優、良、中、不及格.某班50名學生參加測試結果如下:
等級 | 優(86~100分) | 良(75~85分) | 中(60~74分) | 不及格(1~59分) |
人數 | 5 | 21 | 22 | 2 |
(1)估計該班學生體育測試的平均成績;
(2)從該班任意抽取1名學生,求這名學生的測試成績為“優”或“良”的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某大學高等數學這學期分別用![]() 兩種不同的數學方式試驗甲、乙兩個大一新班(人數均為
兩種不同的數學方式試驗甲、乙兩個大一新班(人數均為![]() 人,入學數學平均分和優秀率都相同;勤奮程度和自覺性都一樣).現隨機抽取甲、乙兩班各
人,入學數學平均分和優秀率都相同;勤奮程度和自覺性都一樣).現隨機抽取甲、乙兩班各![]() 名的高等數學期末考試成績,得到莖葉圖:
名的高等數學期末考試成績,得到莖葉圖:
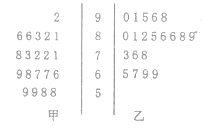
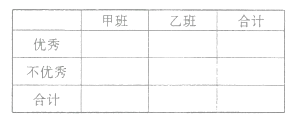
(1)學校規定:成績不得低于85分的為優秀,請填寫下面的![]() 列聯表,并判斷“能否在犯錯誤率的概率不超過0.025的前提下認為成績優異與教學方式有關?”
列聯表,并判斷“能否在犯錯誤率的概率不超過0.025的前提下認為成績優異與教學方式有關?”
下面臨界值表僅供參考:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(參考方式:![]() ,其中
,其中![]() )
)
(2)現從甲班高等數學成績不得低于80分的同學中隨機抽取兩名同學,求成績為86分的同學至少有一個被抽中的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠采用甲、乙兩種不同生產方式生產某零件,現對兩種生產方式所生產的這種零件的產品質量進行對比,其質量按測試指標可劃分為:指標在區間![]() 100的為一等品;指標在區間
100的為一等品;指標在區間![]() 的為二等品
的為二等品![]() 現分別從甲、乙兩種不同生產方式所生產的零件中,各自隨機抽取100件作為樣本進行檢測,測試指標結果的頻率分布直方圖如圖所示:
現分別從甲、乙兩種不同生產方式所生產的零件中,各自隨機抽取100件作為樣本進行檢測,測試指標結果的頻率分布直方圖如圖所示:
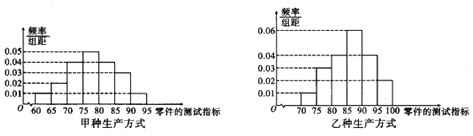
![]() 若在甲種生產方式生產的這100件零件中按等級,利用分層抽樣的方法抽取10件,再從這10件零件中隨機抽取3件,求至少有1件一等品的概率;
若在甲種生產方式生產的這100件零件中按等級,利用分層抽樣的方法抽取10件,再從這10件零件中隨機抽取3件,求至少有1件一等品的概率;
![]() 將頻率分布直方圖中的頻率視作概率,用樣本估計總體
將頻率分布直方圖中的頻率視作概率,用樣本估計總體![]() 若從該廠采用乙種生產方式所生產的所有這種零件中隨機抽取3件,記3件零件中所含一等品的件數為X,求X的分布列及數學期望.
若從該廠采用乙種生產方式所生產的所有這種零件中隨機抽取3件,記3件零件中所含一等品的件數為X,求X的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為考察某種疫苗預防疾病的效果,進行動物試驗,得到統計數據如下:現從所有試驗動物中任取一只,取到“注射疫苗”動物的概率為![]() .
.
未發病 | 發病 | 總計 | |
未注射疫苗 | 20 | x | A |
注射疫苗 | 40 | y | B |
總計 | 60 | 40 | 100 |
(1)求2×2列聯表中的數據x,y,A,B的值.
(2)能否在犯錯誤的概率不超過0.01的前提下認為疫苗有效?
附:![]()
臨界值表:
P(K2≥k0) | 0.05 | 0.01 | 0.005 | 0.001 |
k0 | 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com