
已知數集![]() 具有性質
具有性質![]() ;對任意的
;對任意的
![]() ,
,![]() 與
與![]() 兩數中至少有一個屬于
兩數中至少有一個屬于![]() 。
。
(Ⅰ)分別判斷數集![]() 與
與![]() 是否具有性質
是否具有性質![]() ,并說明理由;
,并說明理由;
(Ⅱ)證明:![]() ,且
,且![]() ;
;
(Ⅲ)證明:當![]() 時,
時,![]() 成等比數列。
成等比數列。
(Ⅰ)由于![]() 與
與![]() 均不屬于數集
均不屬于數集![]() ,∴該數集不具有性質P; 由于
,∴該數集不具有性質P; 由于![]() 都屬于數集
都屬于數集![]() ,∴該數集具有性質P。
,∴該數集具有性質P。
(Ⅱ)證明見解析。
(Ⅲ)證明見解析。
本題主要考查集合、等比數列的性質,考查運算能力、推理論證能力、分
分類討論等數學思想方法。本題是數列與不等式的綜合題,屬于較難層次題。
(Ⅰ)由于![]() 與
與![]() 均不屬于數集
均不屬于數集![]() ,∴該數集不具有性質P;由于
,∴該數集不具有性質P;由于![]() 都屬于數集
都屬于數集![]() , ∴該數集具有性質P。
, ∴該數集具有性質P。
(Ⅱ)∵![]() 具有性質P,∴
具有性質P,∴![]() 與
與![]() 中至少有一個屬于A,
中至少有一個屬于A,
由于![]() ,∴
,∴![]() ,故
,故![]() 。
。
從而![]() ,∴
,∴![]() 。
。
∵![]() , ∴
, ∴![]() ,故
,故![]() 。
。
由A具有性質P可知![]() 。
。
又∵![]() ,
,
∴![]() ,
,
從而![]() ,
,
∴![]() 。
。
(Ⅲ)由(Ⅱ)知,當![]() 時,有
時,有![]() ,即
,即![]() ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
由A具有性質P可知![]() 。
。
由![]() ,得
,得![]() ,且
,且![]() ,∴
,∴![]() ,
,
∴![]() ,即
,即![]() 是首項為1,公比為
是首項為1,公比為![]() 成等比數列。
成等比數列。


 手拉手全優練考卷系列答案
手拉手全優練考卷系列答案科目:高中數學 來源: 題型:
| aj |
| ai |
| a1+a2+…+an | ||||||
|
查看答案和解析>>
科目:高中數學 來源:2009高考真題匯編3-數列 題型:解答題
已知數集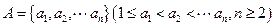 具有性質
具有性質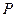 ;對任意的
;對任意的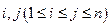 ,
,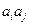 與
與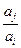 兩數中至少有一個屬于
兩數中至少有一個屬于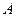 。
。
(Ⅰ)分別判斷數集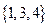 與
與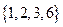 是否具有性質
是否具有性質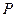 ,并說明理由;
,并說明理由;
(Ⅱ)證明: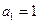 ,且
,且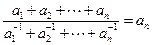 ;
;
(Ⅲ)證明:當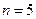 時,
時,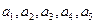 成等比數列。
成等比數列。
查看答案和解析>>
科目:高中數學 來源:2012-2013學年江蘇省高三下學期期中考試數學試卷(解析版) 題型:解答題
已知數集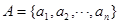 ,其中
,其中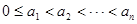 ,且
,且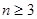 ,若對
,若對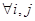 (
(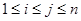 ),
),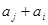 與
與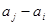 兩數中至少有一個屬于
兩數中至少有一個屬于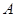 ,則稱數集
,則稱數集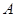 具有性質
具有性質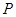 .
.
(Ⅰ)分別判斷數集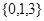 與數集
與數集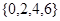 是否具有性質
是否具有性質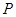 ,說明理由;
,說明理由;
(Ⅱ)已知數集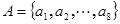 具有性質
具有性質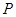 ,判斷數列
,判斷數列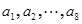 是否為等差數列,若是等差數列,請證明;若不是,請說明理由.
是否為等差數列,若是等差數列,請證明;若不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源:云南省2010-2011學年高三數學一輪復習測試:數列(2) 題型:解答題
已知數集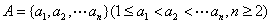 具有性質
具有性質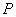 ;對任意的
;對任意的
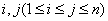 ,
,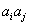 與
與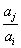 兩數中至少有一個屬于
兩數中至少有一個屬于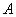 。
。
(I)分別判斷數集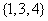 與
與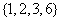 是否具有性質
是否具有性質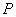 ,并說明理由;
,并說明理由;
(Ⅱ)證明: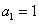 ,且
,且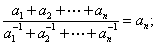
(Ⅲ)證明:當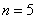 時,
時,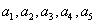 成等比數列。
成等比數列。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com