
【題目】已知兩點![]() ,
,![]() ,若直線
,若直線![]() 上存在四個點
上存在四個點![]() ,使得
,使得![]() 是直角三角形,則實數
是直角三角形,則實數![]() 的取值范圍是( )
的取值范圍是( )
A.![]() B.
B.![]()
C.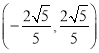 D.
D.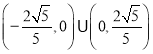
 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】下列四個命題:
![]() 函數
函數![]() 的最大值為1;
的最大值為1;
![]() “
“![]() ,
,![]() ”的否定是“
”的否定是“![]() ”;
”;
![]() 若
若![]() 為銳角三角形,則有
為銳角三角形,則有![]() ;
;
![]() “
“![]() ”是“函數
”是“函數![]() 在區間
在區間![]() 內單調遞增”的充分必要條件.
內單調遞增”的充分必要條件.
其中錯誤的個數是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了改善空氣質量,某市規定,從2018年1月1日起,對二氧化碳排放量超過![]() 的輕型汽車進行懲罰性征稅.檢測單位對甲乙兩品牌輕型汽車各抽取5輛進行二氧化碳排放量檢測,記錄如下:(單位:
的輕型汽車進行懲罰性征稅.檢測單位對甲乙兩品牌輕型汽車各抽取5輛進行二氧化碳排放量檢測,記錄如下:(單位:![]() )
)
甲 | 80 | 110 | 120 | 140 | 150 |
乙 | 100 | 120 |
| 100 | 160 |
經測算得乙品牌輕型汽車二氧化碳排放量的平均值為![]() .
.
(1)求表中![]() 的值,并比較甲乙兩品牌輕型汽車二氧化碳排放量的穩定性;
的值,并比較甲乙兩品牌輕型汽車二氧化碳排放量的穩定性;
(2)從被檢測的5輛甲品牌汽車中隨機抽取2輛,求至少有1輛二氧化碳排放量超過![]() 的概率.(注:方差
的概率.(注:方差![]() ,其中
,其中![]() 為
為![]() 的平均數).
的平均數).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知某運動員每次投籃命中的概率都是40%.現采用隨機模擬的方法估計該運動員三次投籃恰有一次命中的概率:先由計算器產生0到9之間取整數值的隨機數,指定1,2,3,4表示命中,5,6,7,8,9,0表示不命中;再以每三個隨機數作為一組,代表三次投籃的結果.經隨機模擬產生了如下20組隨機數:907,966,191,925,271,932,812,458,569,683,431,257,393,027,556,488,730,113,537,989.據此估計,該運動員三次投籃恰有兩次命中的概率為( )
A.0.25B.0.2C.0.35D.0.4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市約有20萬住戶,為了節約能源,擬出臺“階梯電價”制度,即制定住戶月用電量的臨界值![]() ,若某住戶某月用電量不超過
,若某住戶某月用電量不超過![]() 度,則按平價(即原價)0.5(單位:元/度)計費;若某月用電量超過
度,則按平價(即原價)0.5(單位:元/度)計費;若某月用電量超過![]() 度,則超出部分按議價
度,則超出部分按議價![]() (單位:元/度)計費,未超出部分按平價計費.為確定
(單位:元/度)計費,未超出部分按平價計費.為確定![]() 的值,隨機調查了該市100戶的月用電量,統計分析后得到如圖所示的頻率分布直方圖.根據頻率分布直方圖解答以下問題(同一組數據用該區間的中點值作代表).
的值,隨機調查了該市100戶的月用電量,統計分析后得到如圖所示的頻率分布直方圖.根據頻率分布直方圖解答以下問題(同一組數據用該區間的中點值作代表).
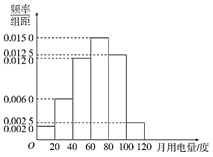
(1)若該市計劃讓全市![]() 的住戶在“階梯電價”出臺前后繳納的電費不變,求臨界值
的住戶在“階梯電價”出臺前后繳納的電費不變,求臨界值![]() ;
;
(2)在(1)的條件下,假定出臺“階梯電價”之后,月用電量未達![]() 度的住戶用電量保持不變;月用電量超過
度的住戶用電量保持不變;月用電量超過![]() 度的住戶節省“超出部分”的
度的住戶節省“超出部分”的![]() ,試估計全市每月節約的電量;
,試估計全市每月節約的電量;
(3)在(1)(2)條件下,若出臺“階梯電價”前后全市繳納電費總額不變,求議價![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為 (
(![]() 為參數),以坐標原點為極點,
為參數),以坐標原點為極點,![]() 軸正半軸為極軸建立極坐標系,直線
軸正半軸為極軸建立極坐標系,直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求直線![]() 和曲線
和曲線![]() 的普通方程;
的普通方程;
(2)已知點![]() ,且直線
,且直線![]() 和曲線
和曲線![]() 交于
交于![]() 兩點,求
兩點,求![]() 的值
的值
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】過點![]() 作圓
作圓![]() 的兩條切線,切點分別為
的兩條切線,切點分別為![]() 、
、![]() ,給出下列四個結論:
,給出下列四個結論:
①![]() ;
;
②若![]() 為直角三角形,則
為直角三角形,則![]() ;
;
③![]() 外接圓的方程為
外接圓的方程為![]() ;
;
④直線![]() 的方程為
的方程為![]() .
.
其中所有正確結論的序號為( )
A.②④B.③④C.②③D.①②④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]()
![]() 的長軸長是短軸長的兩倍,焦距為
的長軸長是短軸長的兩倍,焦距為![]() .
.
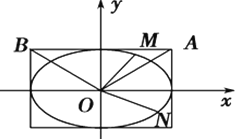
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)不過原點![]() 的直線與橢圓
的直線與橢圓![]() 交于兩點
交于兩點![]() 、
、![]() ,且直線
,且直線![]() 、
、![]() 、
、![]() 的斜率依次成等比數列,問:直線是否定向的,請說明理由.
的斜率依次成等比數列,問:直線是否定向的,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
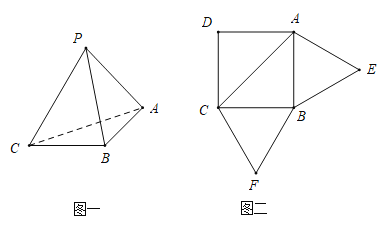
【題目】已知三棱錐![]() 的展開圖如圖二,其中四邊形
的展開圖如圖二,其中四邊形![]() 為邊長等于
為邊長等于![]() 的正方形,
的正方形,![]() 和
和![]() 均為正三角形,在三棱錐
均為正三角形,在三棱錐![]() 中:
中:
(1)證明:平面![]() 平面
平面![]() ;
;
(2)若![]() 是
是![]() 的中點,求二面角
的中點,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com