
【題目】下列四個命題:
![]() 函數
函數![]() 的最大值為1;
的最大值為1;
![]() “
“![]() ,
,![]() ”的否定是“
”的否定是“![]() ”;
”;
![]() 若
若![]() 為銳角三角形,則有
為銳角三角形,則有![]() ;
;
![]() “
“![]() ”是“函數
”是“函數![]() 在區間
在區間![]() 內單調遞增”的充分必要條件.
內單調遞增”的充分必要條件.
其中錯誤的個數是( )
A.1B.2C.3D.4
 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】如圖,已知扇形![]() 是一個觀光區的平面示意圖,其中扇形半徑為10米,
是一個觀光區的平面示意圖,其中扇形半徑為10米,![]() ,為了便于游客觀光和旅游,提出以下兩種設計方案:
,為了便于游客觀光和旅游,提出以下兩種設計方案:
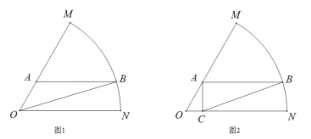
(1)如圖1,擬在觀光區內規劃一條三角形![]() 形狀的道路,道路的一個頂點
形狀的道路,道路的一個頂點![]() 在弧
在弧![]() 上,另一頂點
上,另一頂點![]() 在半徑
在半徑![]() 上,且
上,且![]() ,求
,求![]() 周長的最大值;
周長的最大值;
(2)如圖2,擬在觀光區內規劃一個三角形區域種植花卉,三角形花圃![]() 的一個頂點
的一個頂點![]() 在弧
在弧![]() 上,另兩個頂點
上,另兩個頂點![]()
![]() 在半徑
在半徑![]()
![]() 上,且
上,且![]() ,
,![]() ,求花圃
,求花圃![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】中國古代數學名草《周髀算經》曾記載有“勾股各自乘,并而開方除之”,用符號表示為![]() ,我們把a,b,c叫做勾股數.下列給出幾組勾股數:3,4,5;5,12,13;7,24,25;9,40,41,以此類推,可猜測第5組股數的三個數依次是________.
,我們把a,b,c叫做勾股數.下列給出幾組勾股數:3,4,5;5,12,13;7,24,25;9,40,41,以此類推,可猜測第5組股數的三個數依次是________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】至2018年底,我國發明專利申請量已經連續8年位居世界首位,下表是我國2012年至2018年發明專利申請量以及相關數據.
總計 | ||||||||
年代代碼 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 28 |
申請量 | 65 | 82 | 92 | 110 | 133 | 138 | 154 | 774 |
| 65 | 164 | 276 | 440 | 665 | 828 | 1078 | 3516 |
注:年代代碼1~7分別表示2012~2018.
(1)可以看出申請量每年都在增加,請問這幾年中那一年的增長率達到最高,最高是多少?
(2)建立![]() 關于
關于![]() 的回歸直線方程(精確到0.01),并預測我國發明專利申請量突破200萬件的年份.
的回歸直線方程(精確到0.01),并預測我國發明專利申請量突破200萬件的年份.
參考公式: .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知曲線
中,已知曲線![]() 的參數方程為
的參數方程為 ,以坐標原點
,以坐標原點![]() 為極點,
為極點,![]() 軸正半軸為極軸建立極坐標系,曲線
軸正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求曲線![]() 與曲線
與曲線![]() 兩交點所在直線的極坐標方程;
兩交點所在直線的極坐標方程;
(2)若直線![]() 的極坐標方程為
的極坐標方程為![]() ,直線
,直線![]() 與
與![]() 軸的交點為
軸的交點為![]() ,與曲線
,與曲線![]() 相交于
相交于![]() 兩點,求
兩點,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近來天氣變化無常,陡然升溫、降溫幅度大于![]() 的天氣現象出現增多.陡然降溫幅度大于
的天氣現象出現增多.陡然降溫幅度大于![]() 容易引起幼兒傷風感冒疾病.為了解傷風感冒疾病是否與性別有關,在某婦幼保健院隨機對人院的
容易引起幼兒傷風感冒疾病.為了解傷風感冒疾病是否與性別有關,在某婦幼保健院隨機對人院的![]() 名幼兒進行調查,得到了如下的列聯表,若在全部
名幼兒進行調查,得到了如下的列聯表,若在全部![]() 名幼兒中隨機抽取
名幼兒中隨機抽取![]() 人,抽到患傷風感冒疾病的幼兒的概率為
人,抽到患傷風感冒疾病的幼兒的概率為![]() ,
,
(1)請將下面的列聯表補充完整;
患傷風感冒疾病 | 不患傷風感冒疾病 | 合計 | |
男 | 25 | ||
女 | 20 | ||
合計 | 100 |
(2)能否在犯錯誤的概率不超過![]() 的情況下認為患傷風感冒疾病與性別有關?說明你的理由;
的情況下認為患傷風感冒疾病與性別有關?說明你的理由;
(3)已知在患傷風感冒疾病的![]() 名女性幼兒中,有
名女性幼兒中,有![]() 名又患黃痘病.現在從患傷風感冒疾病的
名又患黃痘病.現在從患傷風感冒疾病的![]() 名女性中,選出
名女性中,選出![]() 名進行其他方面的排查,記選出患黃痘病的女性人數為
名進行其他方面的排查,記選出患黃痘病的女性人數為![]() ,求
,求![]() 的分布列以及數學期望.下面的臨界值表供參考:
的分布列以及數學期望.下面的臨界值表供參考:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
參考公式: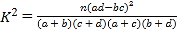 ,其中
,其中![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在極坐標系中,已知曲線![]() :
:![]() 和曲線
和曲線![]() :
:![]() ,以極點
,以極點![]() 為坐標原點,極軸為
為坐標原點,極軸為![]() 軸非負半軸建立平面直角坐標系.
軸非負半軸建立平面直角坐標系.
(1)求曲線![]() 和曲線
和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若點![]() 是曲線
是曲線![]() 上一動點,過點
上一動點,過點![]() 作線段
作線段![]() 的垂線交曲線
的垂線交曲線![]() 于點
于點![]() ,求線段
,求線段![]() 長度的最小值.
長度的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某茶樓有四類茶飲,假設為顧客準備泡茶工具所需的時間互相獨立,且都是整數分鐘,經統計以往為100位顧客準備泡茶工具所需的時間![]() ,結果如下:
,結果如下:
類別 | 鐵觀音 | 龍井 | 金駿眉 | 大紅袍 |
顧客數(人) | 20 | 30 | 40 | 10 |
時間 | 2 | 3 | 4 | 6 |
注:服務員在準備泡茶工具時的間隔時間忽略不計,并將頻率視為概率.
(1)求服務員恰好在第6分種開始準備第三位顧客的泡茶工具的概率;
(2)用![]() 表示至第4分鐘末已準備好了工具的顧客人數,求
表示至第4分鐘末已準備好了工具的顧客人數,求![]() 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com