日日干狠狠干,欧美日韩精品,男女av在线

精英家教網 > 高中數學 > 題目詳情

8．已知點A（1，1），B（-2，2），則向量$\overrightarrow{OA}$與$\overrightarrow{BO}$的夾角為（　　）（其中O為坐標原點）

A．

30°

B．

90°

C．

60°

D．

120°

分析由已知點的坐標求出向量$\overrightarrow{OA}$與$\overrightarrow{BO}$的坐標，結合$\overrightarrow{OA}•\overrightarrow{BO}=0$得答案．

解答解：由A（1，1），B（-2，2），得$\overrightarrow{OA}=（1，1），\overrightarrow{BO}=（2，-2）$，
∴$\overrightarrow{OA}•\overrightarrow{BO}=0$，則向量$\overrightarrow{OA}$與$\overrightarrow{BO}$的夾角為90°．
故選：B．

點評本題考查平面向量的數量積運算，考查向量垂直與夾角的關系，是基礎題．

練習冊系列答案

小學語文詞語手冊吉林教育出版社系列答案

年級	高中課程	年級	初中課程
高一	高一免費課程推薦！	初一	初一免費課程推薦！
高二	高二免費課程推薦！	初二	初二免費課程推薦！
高三	高三免費課程推薦！	初三	初三免費課程推薦！
更多初中、高中輔導課程推薦,點擊進入>>

相關習題

科目：高中數學 來源： 題型：填空題

18．

在梯形ABCD中，AD∥BC，∠ABC=90°，AB=a，AD=3a，且∠ADC=arcsin$\frac{{\sqrt{5}}}{5}$，PA⊥平面ABCD，PA=a，則二面角P-CD-A的大小為arctan$\frac{\sqrt{5}}{3}$．

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

19．2015年5月1日世界博覽會在意大利的米蘭開幕，中國館為了做好世界博覽會期間的接待服務工作，從5名男大學生和3名女大學生中選出3人，參加博覽會的志愿者服務活動．
（Ⅰ）求選出的3人中至少1名女生的概率；
（Ⅱ）設所選3人中女生人數為ξ，求ξ的分布列及數學期望．

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

16．已知向量$\overrightarrow{a}$=（$\sqrt{3}$cosωx，1），$\overrightarrow{b}$=（sinωx，cos²ωx-$\frac{1}{2}$）（ω＞0），函數f（x）=$\overrightarrow{a}•\overrightarrow{b}$，若函數f（x）的圖象的一條對稱軸與它相鄰的一個對稱中心的距離為$\frac{π}{4}$．
（1）求f（x）的表達式；
（2）將函數f（x）的圖象向右平移$\frac{π}{4}$個單位，再將各點的橫坐標縮短到原來的$\frac{1}{2}$（縱坐標不變），得到函數y=g（x）的圖象，求函數g（x）在區間$[0，\frac{π}{4}]$上的最大值和最小值．

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

3．

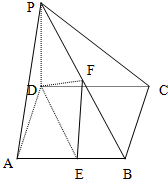如圖，在四棱錐P-ABCD中，PD⊥底面ABCD，底面ABCD為正方體，PD=CD=2，E、F分別是AB、PB的中點
（1）求證：EF⊥CD；
（2）求DB與平面DEF所成角的大小；
（3）在平面PAD內求一點G，使GF⊥平面PCB，并證明你的結論．

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

13．

過曲線C：y=e^x上一點P₀（0，1）作曲線C的切線l₀交x軸于點Q₁（x₁，0），又過Q₁作x軸的垂線交曲線C于點P₁（x₁，y₁），然后再過P₁（x₁，y₁）作曲線C的切線l₁交x軸于點Q₂（x₂，0），又過Q₂作x軸的垂線交曲線C于點P₂（x₂，y₂），…，以此類推，過點P_n的切線l_n與x軸相交于點
Q_n+1（x_n+1，0），再過點Q_n+1作x軸的垂線交曲線C于點P_n+1（x_n+1，y_n+1）（n∈N^*）．
（1）求x₁、x₂及數列{x_n}的通項公式；
（2）設曲線C與切線l_n及直線P_n+1Q_n+1所圍成的圖形面積為S_n，求S_n的表達式；
（3）在滿足（2）的條件下，若數列{S_n}的前n項和為T_n，求證：$\frac{{T}_{n+1}}{{T}_{n}}$＜$\frac{{x}_{n+1}}{{x}_{n}}$（n∈N₊）．

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

20．

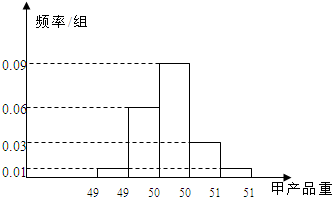某食品廠為了檢查甲、乙兩條自動包裝流水線的生產情況，隨機在這兩條流水線上各抽取40件產品作為樣本．經統計，得到關于產品重量的樣本頻率分布直方圖和樣本頻數分布表：

乙流水線產品重量（單位：克）	頻數
（490，495]	6
（495，500]	8
（500，505]	14
（505，510]	8
（510，515]	4

已知產品的重量合格標準為：重量值落在（495，510]內的產品為合格品；否則為不合格品．
（1）從甲流水線樣本的合格品中任意取2件，求重量值落在（505，510]的產品件數X的分布列；
（2）從乙流水線中任取2件產品，試根據樣本估計總體的思想，求其中合格品的件數Y的數學期望；
（3）從甲、乙流水線中各取2件產品，用ξ表示“甲流水線合格品數與乙流水線合格品數的差的絕對值”，并用A表示事件“關于x的一元二次方程2x²+2ξx+ξ=0沒有實數解”．試根據樣本估計總體的思想，求事件A的概率．

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

17．已知一個口袋中裝有n個紅球（n≥1且n∈N）和2個白球，從中有放回地連續摸三次，每次摸出兩個球，若兩個球顏色不同則為中獎，否則不中獎．
（1）當n=3時，設三次摸球中（每次摸球后放回）中獎的次數為ξ，求的ξ分布列；
（2）記三次摸球中（每次摸球后放回）恰有兩次中獎的概率為P，當n取多少時，P最大．

查看答案和解析>>

科目：高中數學 來源： 題型：填空題

18．已知函數$f（x）=\left\{\begin{array}{l}{x^2}+2x-3，x≤0\\ lnx-a，x＞0\end{array}\right.（a∈R）$，若關于x的方程f（x）=k有三個不等的實根，則實數k的取值范圍是（-4，-3）．

查看答案和解析>>

同步練習冊答案

日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

練習冊

高中

初中

小學