【題目】如圖，在
中，
，P為AB上一動點，
交于AC于點D，現將
沿PD翻折至
，使平面
平面PBCD.
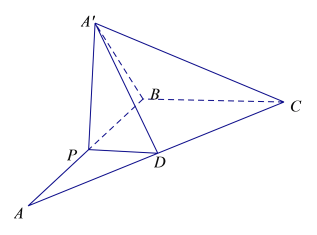
（1）若
，求棱錐
的體積；
（2）若點P為AB的中點，求證：平面
平面
.
科目：高中數學 來源： 題型：
【題目】已知橢圓
的中心在坐標原點，焦點在
軸上，離心率為
，橢圓上的點到焦點距離的最大值為
．
（Ⅰ）求橢圓的標準方程；
（Ⅱ）若過點
的直線
與橢圓交于不同的兩點
，且
，求實數
的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某校舉行“慶元旦”教工羽毛球單循環比賽（任意兩個參賽隊伍只比賽一場），有高一、高二、高三共三個隊參賽，高一勝高二的概率為
，高一勝高三的概率為
，高二勝高三的概率為
，每場勝負相互獨立，勝者記1分，負者記0分，規定：積分相同時，高年級獲勝.
（1）若高三獲得冠軍的概率為
，求
；
（2）記高三的得分為
，求
的分布列和期望.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某學校為調查高二學生上學路程所需要的時間（單位：分鐘），從高二年級學生中隨機抽取
名按上學所需要時間分組：第
組
，第
組
，第
組
，第
組
，第
組
，得到的頻率分布直方圖如圖所示．
（
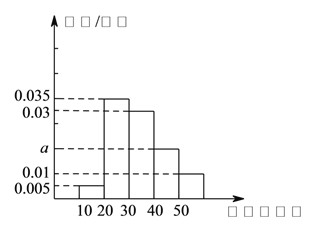
）根據圖中數據求
的值．
（
）若從第
， 
， 
組中用分層抽樣的方法抽取
名新生參與交通安全問卷調查，應從第
， 
， 
組各抽取多少名新生？
（
）在（
）的條件下，該校決定從這
名學生中隨機抽取
名新生參加交通安全宣傳活動，求第
組至少有一志愿者被抽中的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：
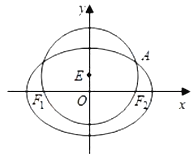
【題目】已知圓
： 
經過橢圓
： 
的左右焦點
，且與橢圓
在第一象限的交點為
，且
三點共線，直線
交橢圓
于
， 
兩點，且
（
）.
（1）求橢圓
的方程；
（2）當三角形
的面積取得最大值時，求直線
的方程.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在四棱錐O﹣ABCD中，OA⊥底面ABCD，且底面ABCD是邊長為2的正方形，且OA＝2，M，N分別為OA，BC的中點.
（1）求證：直線MN
平面OCD；
（2）求點B到平面DMN的距離.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某工廠擬建一座平面圖(如右圖所示)為矩形且面積為200平方米的三級污水處理池，由于地形限制，長、寬都不能超過16米，如果池外周壁建造單價為每米400元，中間兩條隔墻建造單價為每米248元，池底建造單價為每平方米80元(池壁厚度忽略不計，且池無蓋)．
(1)寫出總造價y(元)與污水處理池長x(米)的函數關系式，并指出其定義域；
(2)求污水處理池的長和寬各為多少時，污水處理池的總造價最低？并求最低總造價．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖所示，已知棱錐P-ABC 中.PA⊥平面ABC，AB⊥AC，PA=AC=
AB=1，N為AB 上一點，AB=4AN，M.S分別為PB，BC的中點.
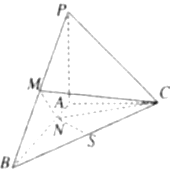
（1）證明：CM⊥SN；
（2）求二面角M-NC-B的余弦值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為監控某種零件的一條生產線的生產過程，檢驗員每天從該生產線上隨機抽取10個零件，度量其內徑尺寸（單位：
）.根據長期生產經驗，可以認為這條生產線正常狀態下生產的零件的內徑尺寸服從正態分布
.
（1）假設生產狀態正常，記X表示某一天內抽取的10個零件中其內徑尺寸在
之外的零件數，求
及X的數學期望；
（2）某天正常工作的一條生產線數據記錄的莖葉圖如下圖所示：
①計算這一天平均值
與標準差
；
②一家公司引進了一條這種生產線，為了檢查這條生產線是否正常，用這條生產線試生產了5個零件，度量其內徑分別為（單位：）：95，103，109，112，119，試問此條生產線是否需要進一步調試，為什么？
參考數據：
，
，
，
，
，
，
，
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
