
【題目】已知函數f(x)=a1nx﹣ax+1(a∈R且a≠0).
(1)求函數f(x)的單調區間;
(2)求證:![]() (n≥2,n∈N*).
(n≥2,n∈N*).
【答案】(1)當a>0時, f(x)的單調遞增區間(0,1),單調遞減區間(1,+∞);
當a<0時, f(x)的單調遞減區間(0,1),單調遞增區間(1,+∞);
(2)證明,見解析
【解析】
(1)對f(x)求導,分a>0,a<0兩種情況討論,分析函數單調性即可;
(2)令a=1,由(1)可證得lnx<x﹣1,即![]() ,疊乘可得證.
,疊乘可得證.
(1)∵f(x)=a1nx﹣ax+1,∴f′(x)![]() a
a![]() ,
,
①當a>0時,
若0<x<1,則f′(x)>0,若x>1,f′(x)<0,
∴f(x)的單調遞增區間(0,1),單調遞減區間(1,+∞);
②當a<0時,
若0<x<1,則f′(x)<0,若x>1,f′(x)>0,
∴f(x)的單調遞減區間(0,1),單調遞增區間(1,+∞);
(2)令a=1,則f(x)=lnx﹣x+1,所以f(1)=0,
由(1)可知f(x)在[1,+∞)單調遞減,
故f(x)≤f(1),(當x=1時取等號),
所以lnx﹣x+1<0,即lnx<x﹣1,
從而有0<lnn<n﹣1,(n≥2,n∈N*),
即![]() (n≥2,n∈N*),
(n≥2,n∈N*),
∴![]() (n≥2,n∈N*).
(n≥2,n∈N*).


 金牌教輔培優優選卷期末沖刺100分系列答案
金牌教輔培優優選卷期末沖刺100分系列答案科目:高中數學 來源: 題型:
【題目】已知極點與平面直角坐標系的原點重合,極軸與![]() 軸的正半軸重合,直線
軸的正半軸重合,直線![]() 的參數方程為
的參數方程為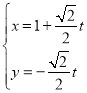 (
(![]() 是參數),曲線
是參數),曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求直線![]() 的普通方程與曲線
的普通方程與曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)設直線![]() 與曲線
與曲線![]() 交于
交于![]() ,
,![]() 兩點,點
兩點,點![]() 為曲線
為曲線![]() 上一點,求使
上一點,求使![]() 面積取得最大值時的
面積取得最大值時的![]() 點坐標.
點坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() ,(
,(![]() 為參數),以坐標原點為極點,
為參數),以坐標原點為極點,![]() 軸的正半軸為極軸,建立極坐標系,曲線
軸的正半軸為極軸,建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)寫出曲線![]() 的極坐標方程和曲線
的極坐標方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若射線![]() 與曲線
與曲線![]() 相交于點
相交于點![]() ,將
,將![]() 逆時針旋轉
逆時針旋轉![]() 后,與曲線
后,與曲線![]() 相交于點
相交于點![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某產品的廣告支出![]() (單位:萬元)與銷售收入
(單位:萬元)與銷售收入![]() (單位:萬元)之間有下表所對應的數據:
(單位:萬元)之間有下表所對應的數據:
廣告支出 | 1 | 2 | 3 | 4 |
銷售收入 | 12 | 28 | 42 | 56 |
(1)畫出表中數據的散點圖;
(2)求出![]() 對
對![]() 的線性回歸方程;
的線性回歸方程;
(3)若廣告費為9萬元,則銷售收入約為多少萬元?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】先后2次拋擲一枚骰子,將得到的點數分別記為![]() ,
,![]() .
.
(1)求直線![]() 與圓
與圓![]() 相切的概率;
相切的概率;
(2)將![]() ,
,![]() ,5的值分別作為三條線段的長,求這三條線段能圍成等腰三角形的概率.
,5的值分別作為三條線段的長,求這三條線段能圍成等腰三角形的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com