Question

17．已知實(shí)數(shù)x，y滿足$\left\{\begin{array}{l}{x≥-3}\\{y≤2}\\{x-y-1≤0}\end{array}\right.$，則$\frac{y-1}{x-4}$的最大值為$\frac{5}{7}$．

Answer 1

分析 由約束條件作出可行域，再由$\frac{y-1}{x-4}$的幾何意義，即可行域內(nèi)的動(dòng)點(diǎn)與定點(diǎn)P（4，1）連線的斜率求得答案．

解答 解：由約束條件$\left\{\begin{array}{l}{x≥-3}\\{y≤2}\\{x-y-1≤0}\end{array}\right.$作出可行域如圖，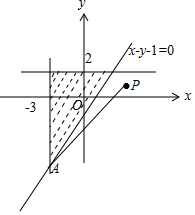

聯(lián)立$\left\{\begin{array}{l}{x=-3}\\{x-y-1=0}\end{array}\right.$，解得A（-3，-4），
$\frac{y-1}{x-4}$的幾何意義為可行域內(nèi)的動(dòng)點(diǎn)與定點(diǎn)P（4，1）連線的斜率，
由圖可知，$\frac{y-1}{x-4}$的最大值為$\frac{-4-1}{-3-4}=\frac{5}{7}$．
故答案為：$\frac{5}{7}$．

點(diǎn)評 本題考查簡單的線性規(guī)劃，考查了數(shù)形結(jié)合的解題思想方法和數(shù)學(xué)轉(zhuǎn)化思想方法，是中檔題．