【題目】在△ABC中，角
，
，
所對的邊分別為
，
，c．已知
．
則角的大小________
【答案】
；
【解析】分析：根據余弦定理，將題中等式化簡整理，可得sinBcosC=2sinAcosB﹣sinCcosB，利用兩角和正弦公式化簡得2sinAcosB=sin（B+C）=sinA，在兩邊約去sinA得
，結合三角形內角取值范圍即可得到角B的大小.
詳解：∵在△ABC中，b2=a2+c2﹣2accosB，
∴b2﹣a2﹣c2=﹣2accosB，同理可得c2﹣a2﹣b2=﹣2abcosC
∵
∴
，
∵sinC≠0，可得sinBcosC=2sinAcosB﹣sinCcosB，
∴2sinAcosB=sinBcosC+sinCcosB=sin（B+C）=sinA，
∵sinA≠0，∴等式兩邊約去sinA，可得，
∵0＜B＜π，∴角B的大小．
新活力總動員暑系列答案
龍人圖書快樂假期暑假作業鄭州大學出版社系列答案科目：高中數學 來源： 題型：
【題目】下列說法錯誤的是（ ）
A.命題“若 
，則 
”的逆否命題為：“若 
，則 
”
B.“ 
”是“ 
”的充分不必要條件
C.若 
且 
為假命題，則 、 均為假命題
D.命題 ：“ 
，使得 
”，則 
：“ 
，均有 
”
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下列命題正確的個數為（ ）
①“x∈R都有x2≥0”的否定是“x0∈R使得x02≤0”；
②“x≠3”是“|x|≠3”成立的充分條件；
③命題“若m≤ 
，則方程mx2+2x+2=0有實數根”的否命題為真命題．
A.0
B.1
C.2
D.3
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設雙曲線 
（a＞0，b＞0）的左焦點為F1 ， 左頂點為A，過F1作x軸的垂線交雙曲線于P、Q兩點，過P作PM垂直QA于M，過Q作QN垂直PA于N，設PM與QN的交點為B，若B到直線PQ的距離大于a+ 
，則該雙曲線的離心率取值范圍是（ ）
A.（1﹣ 
）
B.（ ，+∞）
C.（1，2 ）
D.（2 ，+∞）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某工廠對新研發的一種產品進行試銷，得到如下數據表：
（1）根據上表求出回歸直線方程 
，并預測當單價定為8.3元時的銷量；
（2）如果該工廠每件產品的成本為5.5元，利用所求的回歸方程，要使得利潤最大，單價應該定為多少？
附：線性回歸方程 中斜率和截距最小二乘估計計算公式：
， 
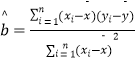查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設橢圓
的右焦點為
，右頂點為
，已知
，其中
為原點，
為橢圓的離心率.
（1）求橢圓的方程；
（2）設過點的直線
與橢圓交于點
（不在
軸上），垂直于的直線與交于點
，與
軸交于點
，若
，且
，求直線的斜率的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某水仙花經營部每天的房租、水電、人工等固定成本為1000元，每盆水仙花的進價是10元，銷售單價
(元) (
)與日均銷售量
(盆)的關系如下表，并保證經營部每天盈利．
| 20 | 35 | 40 | 50 |
| 400 | 250 | 200 | 100 |
| 20 | 35 | 40 | 50 |
| 400 | 250 | 200 | 100 |
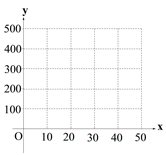
(Ⅰ) 在所給的坐標圖紙中，根據表中提供的數據，描出實數對
的對應點，并確定
與
的函數關系式；
（Ⅱ）求出
的值，并解釋其實際意義；
（Ⅲ）請寫出該經營部的日銷售利潤
的表達式，并回答該經營部怎樣定價才能獲最大日銷售利潤？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
