
設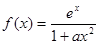 ,其中
,其中
(Ⅰ)當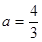 時,求
時,求 的極值點;
的極值點;
(Ⅱ)若 為R上的單調函數,求a的取值范圍。
為R上的單調函數,求a的取值范圍。
(Ⅰ)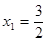 是極小值點,
是極小值點, 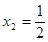 是極大值點(Ⅱ)
是極大值點(Ⅱ)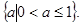
【解析】本試題主要是考查了導數在研究函數中的運用。
(1)對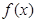 求導得
求導得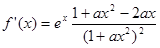 ①
①
(Ⅰ)當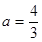 時,若
時,若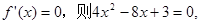
解得 ,判定單調性得到極值。
,判定單調性得到極值。
(2)若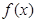 為R上的單調函數,則
為R上的單調函數,則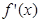 在R上不變號,
在R上不變號,
結合①與條件a>0,知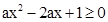 在R上恒成立轉化為不等式恒成立問題來求解參數的范圍。
在R上恒成立轉化為不等式恒成立問題來求解參數的范圍。
解:對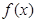 求導得
求導得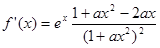 ①……………2分
①……………2分
(Ⅰ)當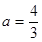 時,若
時,若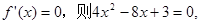
解得 ……………4分
……………4分
綜合①,可知
|
|
|
|
|
|
|
|
|
+ |
0 |
- |
0 |
+ |
|
|
↗ |
極大值 |
↘ |
極小值 |
↗ |
所以, 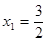 是極小值點,
是極小值點, 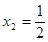 是極大值點. ……………8分
是極大值點. ……………8分
(II)若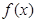 為R上的單調函數,則
為R上的單調函數,則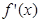 在R上不變號,
在R上不變號,
結合①與條件a>0,知 在R上恒成立,……………10分
在R上恒成立,……………10分
因此 由此并結合
由此并結合 ,知
,知 。
。
所以a的取值范圍為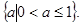 ……………14分
……………14分


科目:高中數學 來源:2012屆湖北省鄂州二中高三十一月份階段性考試理科數學 題型:解答題
(本題滿分12分)設函數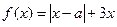 ,其中
,其中 。
。
(Ⅰ)當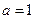 時,求不等式
時,求不等式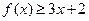 的解集;
的解集;
(Ⅱ)若不等式 的解集為
的解集為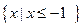 ,求a的值。
,求a的值。
查看答案和解析>>
科目:高中數學 來源:2012-2013學年甘肅省高三(奧班)10月月考理科數學試卷(解析版) 題型:解答題
選修4-5:不等式選講(本小題滿分10分)
設函數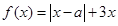 ,其中
,其中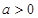 。
。
(Ⅰ)當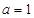 時,求不等式
時,求不等式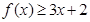 的解集;
的解集;
(Ⅱ)若不等式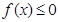 的解集為
的解集為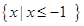 ,求a的值。
,求a的值。
查看答案和解析>>
科目:高中數學 來源:2011-2012學年海南省高三第六次月考理科數學試卷(解析版) 題型:解答題
設函數 ,其中
,其中 。
。
(Ⅰ)當 時,求不等式
時,求不等式 的解集
的解集
(Ⅱ)若不等式 的解集為
的解集為 ,求a的值。
,求a的值。
查看答案和解析>>
科目:高中數學 來源:2011-2012學年新人教版高三一輪復習單元測試(8)數學試卷 題型:解答題
(12分)(理)設函數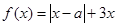 ,其中
,其中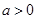 。
。
(Ⅰ)當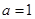 時,求不等式
時,求不等式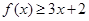 的解集;
的解集;
(Ⅱ)若不等式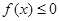 的解集為
的解集為 ,求a的值。
,求a的值。
查看答案和解析>>
科目:高中數學 來源:2011年高考試題數學(全國卷新課標)解析版 題型:解答題
選修4-5:不等式選講
設函數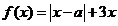 ,其中
,其中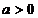 。
。
(Ⅰ)當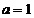 時,求不等式
時,求不等式 的解集;
的解集;
(Ⅱ)若不等式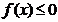 的解集為
的解集為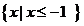 ,求a的值。
,求a的值。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com