
分析 先求出$\overrightarrow{a}+2\overrightarrow{b}$,再由$({\overrightarrow a+2\overrightarrow b})⊥\overrightarrow c$,能求出m.
解答 解:∵向量$\overrightarrow a=({2\sqrt{2},2})$,$\overrightarrow b=({0,2})$,
∴$\overrightarrow a+2\overrightarrow b=({2\sqrt{2},6})$,
∵$\overrightarrow c=({m,\sqrt{2}})$,且$({\overrightarrow a+2\overrightarrow b})⊥\overrightarrow c$,
∴$({\overrightarrow a+2\overrightarrow b})•\overrightarrow c=0$,
解得$2\sqrt{2}m+6\sqrt{2}=0$,解得m=-3.
故答案為:-3.
點評 本題考查實數值的求法,是基礎題,解題時要認真審題,注意向量垂直的性質的合理運用.


 學而優銜接教材南京大學出版社系列答案
學而優銜接教材南京大學出版社系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
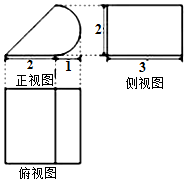
| A. | 4+$\frac{3}{2}$π | B. | 6+$\frac{3}{2}$π | C. | 6+3π | D. | 12+$\frac{3}{2}$π |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 增函數且最小值是-5 | B. | 增函數且最大值是-5 | ||
| C. | 減函數且最大值是-5 | D. | 減函數且最小值是-5 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com