
分析 先求出基本事件總數n=${A}_{6}^{6}$,再求出2個舞蹈節目一起演出包含的基本事件個數,由此能求出2個舞蹈節目一起演出的概率.
解答 解:4個唱歌節目,2個跳舞節目,任意排一張演出節目單,
基本事件總數n=${A}_{6}^{6}$,
2個舞蹈節目一起演出包含的基本事件個數m=${A}_{2}^{2}{A}_{5}^{5}$,
∴2個舞蹈節目一起演出的概率p=$\frac{m}{n}$=$\frac{{A}_{2}^{2}{A}_{5}^{5}}{{A}_{6}^{6}}$=$\frac{1}{3}$.
故答案為:$\frac{1}{3}$.
點評 本題考查概率的求法,是基礎題,解題時要認真審題,注意等可能事件概率計算公式的合理運用.


科目:高中數學 來源: 題型:解答題
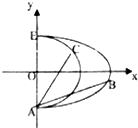 已知曲線C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0,x≥0)和曲線C2:x2+y2=r2(x≥0)都過點A(0,-1),且曲線C1所在的圓錐曲線的離心率為$\frac{\sqrt{3}}{2}$
已知曲線C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0,x≥0)和曲線C2:x2+y2=r2(x≥0)都過點A(0,-1),且曲線C1所在的圓錐曲線的離心率為$\frac{\sqrt{3}}{2}$查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 若A,B,C是平面內的三點,則$\overrightarrow{AB}-\overrightarrow{AC}=\overrightarrow{BC}$ | |
| B. | 若$\overrightarrow{e_1}、\overrightarrow{e_2}$是兩個單位向量,則$\overrightarrow{e_1}=\overrightarrow{e_2}$ | |
| C. | 若$\overrightarrow a、\overrightarrow b$是任意兩個向量,則$|{\overrightarrow a+\overrightarrow b}|≤|{\overrightarrow a}|+|{\overrightarrow b}|$ | |
| D. | 向量$\overrightarrow{e_1}=(0,0),\overrightarrow{e_2}=(1,-2)$可以作為平面內所有向量的一組基底 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
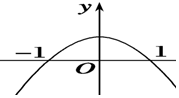 已知f′(x)是f(x)的導數,且y=xf′(x)的圖象如圖所示,則下列關于f(x)說法正確的是( )
已知f′(x)是f(x)的導數,且y=xf′(x)的圖象如圖所示,則下列關于f(x)說法正確的是( )| A. | 在(-∞,0)上是增函數 | B. | 在(-1,1)上是增函數 | ||
| C. | 在(-1,0)上是增函數 | D. | 在(1,+∞)上是減函數 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 奇函數 | B. | 偶函數 | ||
| C. | 非奇非偶函數 | D. | 既是奇函數又是偶函數 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com