Question

8．不等式組$\left\{\begin{array}{l}{0≤2x+y≤6}\\{0≤x-y≤3}\end{array}\right.$表示的平面區域的面積為6．

Answer 1

分析 根據題意畫出不等式組表示的平面區域，結合平面圖形是平行四邊形，求出它的面積即可．

解答 解：畫出不等式組$\left\{\begin{array}{l}{0≤2x+y≤6}\\{0≤x-y≤3}\end{array}\right.$表示的平面區域如圖所示，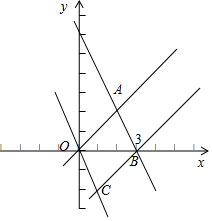

則四邊形OABC是平行四邊形，
由$\left\{\begin{array}{l}{2x+y=6}\\{x-y=0}\end{array}\right.$求得點A（2，2），
由$\left\{\begin{array}{l}{x-y=3}\\{2x+y=6}\end{array}\right.$求得B（3，0）；
所以四邊形OABC的面積為：
S=2S_△OAB=2×$\frac{1}{2}$×3×2=6．
故答案為：6．

點評 本題考查了二元一次不等式組表示平面區域的應用問題，是基礎題目．