
【題目】已知函數![]() .
.
(1)討論![]() 的單調性;
的單調性;
(2)若![]() 有兩個極值點
有兩個極值點![]() ,不等式
,不等式![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)見解析;(2)![]()
【解析】
(1)根據![]() 的取值對導函數的正負的影響分類討論即可.
的取值對導函數的正負的影響分類討論即可.
(2)根據題意,需求![]() 的最值,結合(1)可得
的最值,結合(1)可得![]() 且
且![]() ,于是此式可轉化為關于
,于是此式可轉化為關于![]() 的函數,再利用導數求其最值即可.
的函數,再利用導數求其最值即可.
(1)由題意得![]() ,
,
![]() ,
,
令![]() .
.
①當![]() 時,
時,![]() 恒成立,則
恒成立,則![]() 在
在![]() 上單調遞減.
上單調遞減.
②當![]() 時,
時,![]() ,函數
,函數![]() 與
與![]() 軸有兩個不同的交點
軸有兩個不同的交點![]() ,
,
![]() 則
則![]() ,
,
所以當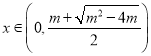 時,
時,![]() 單調遞增;
單調遞增;
當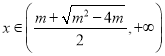 時,
時,![]() 單調遞減.
單調遞減.
③當![]() 時,
時,![]() ,函數
,函數![]() 與
與![]() 軸有兩個不同的交點
軸有兩個不同的交點![]() ,
,
![]() 則
則![]() ,
,
所以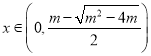 時,
時,![]() 單調遞減;
單調遞減;
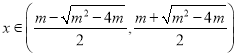 時,
時,![]() 單調遞增;
單調遞增;
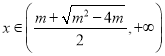 時,
時,![]() 單調遞減.
單調遞減.
綜上所述:當![]() 時,
時,![]() 在
在![]() 上單調遞減.
上單調遞減.
當![]() 時,
時,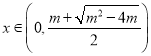 時,
時,![]() 單調遞增;
單調遞增;
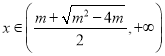 時,
時,![]() 單調遞減.
單調遞減.
當![]() 時,
時,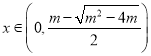 時,
時,![]() 單調遞減;
單調遞減;
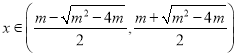 時,
時,![]() 單調遞增;
單調遞增;
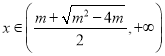 時,
時,![]() 單調遞減.
單調遞減.
(2)由(1)知:![]() 時
時![]() 有兩個極值點
有兩個極值點![]() ,
,
且![]() 為方程
為方程![]() 的兩根,
的兩根,![]()
![]()
![]() .
.
![]() .
.
所以![]() .
.
所以![]() 在
在![]() 時恒成立.
時恒成立.
令![]() ,則
,則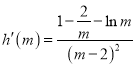 .
.
令![]() 則
則![]() ,
,
所以![]() 在
在![]() 上單調遞減.又
上單調遞減.又![]() ,
,
所以![]() 在
在![]() 上恒成立,即
上恒成立,即![]() .所以
.所以![]() .
.
所以![]() 在
在![]() 上為減函數.所以
上為減函數.所以![]() .
.
所以![]() ,即
,即![]() 的取值范圍是
的取值范圍是![]() .
.


科目:高中數學 來源: 題型:
【題目】已知拋物線![]() 的頂點為原點,其焦點
的頂點為原點,其焦點![]() 到直線
到直線![]() 的距離為
的距離為![]() .設
.設![]() 為直線
為直線![]() 上的點,過點
上的點,過點![]() 作拋物線
作拋物線![]() 的兩條切線
的兩條切線![]() ,其中
,其中![]() 為切點.
為切點.
(1) 求拋物線![]() 的方程;
的方程;
(2) 當點![]() 為直線
為直線![]() 上的定點時,求直線
上的定點時,求直線![]() 的方程;
的方程;
(3) 當點![]() 在直線
在直線![]() 上移動時,求
上移動時,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義:已知函數![]() 在
在![]() 上的最小值為
上的最小值為![]() ,若
,若![]() 恒成立,則稱函數
恒成立,則稱函數![]() 在
在![]() 上具有“
上具有“![]() ”性質.
”性質.
(![]() )判斷函數
)判斷函數![]() 在
在![]() 上是否具有“
上是否具有“![]() ”性質?說明理由.
”性質?說明理由.
(![]() )若
)若![]() 在
在![]() 上具有“
上具有“![]() ”性質,求
”性質,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖是由正整數構成的數表,用aij表示i行第j個數(i,j∈N+).此表中ail=aii=i,每行中除首尾兩數外,其他各數分別等于其“肩膀”上的兩數之和.

(1)寫出數表的第六行(從左至右依次列出).
(2)設第n行的第二個數為bn(n≥2),求bn.
(3)令![]() ,記Tn為數列
,記Tn為數列![]() 前n項和,求
前n項和,求![]() 的最大值,并求此時n的值.
的最大值,并求此時n的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】過拋物線y2=4x焦點F的直線交拋物線于A、B兩點,交其準線于點C,且A、C位于x軸同側,若|AC|=2|AF|,則|BF|等于( )
A. 2B. 3C. 4D. 5
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法中,正確的是( )
A. 命題“若![]() ,則
,則![]() ”的逆命題是真命題
”的逆命題是真命題
B. 命題“存在![]() ”的否定是:“任意
”的否定是:“任意![]() ”
”
C. 命題“p或q”為真命題,則命題“p”和命題“q”均為真命題
D. 已知![]() ,則“
,則“![]() ”是“
”是“![]() ”的充分不必要條件
”的充分不必要條件
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為響應國家“精準扶貧、精準脫貧”的號召,某貧困縣在精準推進上下實功,在在精準落實上見實效現從全縣扶貧對象中隨機抽取![]() 人對扶貧工作的滿意度進行調查,以莖葉圖中記錄了他們對扶貧工作滿意度的分數(滿分
人對扶貧工作的滿意度進行調查,以莖葉圖中記錄了他們對扶貧工作滿意度的分數(滿分![]() 分)如圖所示,已知圖中的平均數與中位數相同.現將滿意度分為“基本滿意”(分數低于平均分)、“滿意”(分數不低于平均分且低于
分)如圖所示,已知圖中的平均數與中位數相同.現將滿意度分為“基本滿意”(分數低于平均分)、“滿意”(分數不低于平均分且低于![]() 分)和“很滿意”(分數不低于
分)和“很滿意”(分數不低于![]() 分)三個級別.
分)三個級別.

(1)求莖葉圖中數據的平均數和![]() 的值;
的值;
(2)從“滿意”和“很滿意”的人中隨機抽取![]() 人,求至少有
人,求至少有![]() 人是“很滿意”的概率.
人是“很滿意”的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com