
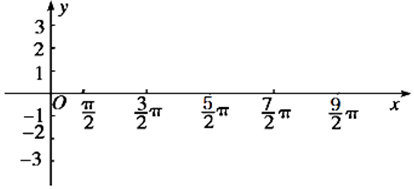
分析 (Ⅰ)根據三角函數圖象平移法則,得出函數y=f(x)的解析式,利用正弦函數的圖象與性質求出f(x)的單調增區間;
(Ⅱ)利用列表、描點、連線的方法得出函數在一個周期的圖象.
解答 解:(Ⅰ)函數y=sin x的圖象向右平移 $\frac{π}{4}$,得到y=sin(x-$\frac{π}{4}$)的圖象;
縱坐標不變,橫坐標伸長為原來的2倍,得到y=sin($\frac{1}{2}$x-$\frac{π}{4}$)的圖象;
橫坐標不變,縱坐標伸長為原來的3倍,得到y=3sin($\frac{1}{2}$x-$\frac{π}{4}$)的圖象;
∴函數y=f(x)=3sin($\frac{1}{2}$x-$\frac{π}{4}$);
令-$\frac{π}{2}$+2kπ≤$\frac{1}{2}$x-$\frac{π}{4}$≤$\frac{π}{2}$+2kπ,k∈Z,
解得-$\frac{π}{2}$+4kπ≤x≤$\frac{3π}{2}$+4kπ,k∈Z,
∴f(x)的單調增區間為[-$\frac{π}{2}$+4kπ,$\frac{3π}{2}$+4kπ],k∈Z;
(Ⅱ)列表如下;
| $\frac{1}{2}$x-$\frac{π}{4}$ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | $\frac{π}{2}$ | $\frac{3π}{2}$ | $\frac{5π}{2}$ | $\frac{7π}{2}$ | $\frac{9π}{2}$ |
| 3sin($\frac{1}{2}$x-$\frac{π}{4}$) | 0 | 3 | 0 | -3 | 0 |
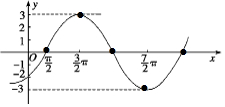
點評 本題考查了三角函數的圖象與性質的應用問題,也l考查了圖象平移與五點法畫圖的問題,是基礎題.


 考前必練系列答案
考前必練系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 2 | B. | 2$\sqrt{2}$ | C. | $\sqrt{7}$ | D. | 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
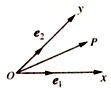 如圖,設Ox、Oy是平面內相交成45°角的兩條數軸,$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$分別是x軸、y軸正方向同向的單位向量,若向量$\overrightarrow{OP}$=x$\overrightarrow{{e}_{1}}$+y$\overrightarrow{{e}_{2}}$,則把有序數對(x,y)叫做向量$\overrightarrow{OP}$在坐標系xOy中的坐標,在此坐標系下,假設$\overrightarrow{OA}$=(-2,2$\sqrt{2}$),$\overrightarrow{OB}$=(2,0),$\overrightarrow{OC}$=(5,-3$\sqrt{2}$),則下列命題不正確的是( )
如圖,設Ox、Oy是平面內相交成45°角的兩條數軸,$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$分別是x軸、y軸正方向同向的單位向量,若向量$\overrightarrow{OP}$=x$\overrightarrow{{e}_{1}}$+y$\overrightarrow{{e}_{2}}$,則把有序數對(x,y)叫做向量$\overrightarrow{OP}$在坐標系xOy中的坐標,在此坐標系下,假設$\overrightarrow{OA}$=(-2,2$\sqrt{2}$),$\overrightarrow{OB}$=(2,0),$\overrightarrow{OC}$=(5,-3$\sqrt{2}$),則下列命題不正確的是( )| A. | $\overrightarrow{{e}_{1}}$=(1,0) | B. | |$\overrightarrow{OA}$|=2$\sqrt{3}$ | C. | $\overrightarrow{OA}$∥$\overrightarrow{BC}$ | D. | $\overrightarrow{OA}$⊥$\overrightarrow{OB}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com