
| A. | -$\frac{2\sqrt{6}}{3}$ | B. | 0 | C. | 1 | D. | $\frac{\sqrt{3}}{3}$ |
分析 由題意可知:設P(x,y),F1(-$\sqrt{3}$,0),F2($\sqrt{3}$,0),則$\overrightarrow{P{F}_{1}}$=(-$\sqrt{3}$-x,-y),$\overrightarrow{P{F}_{2}}$=($\sqrt{3}$-x,-y),$\overrightarrow{P{F}_{1}}•\overrightarrow{P{F}_{2}}$=(-$\sqrt{3}$-x,-y)•($\sqrt{3}$-x,-y)=x2+y2-3,根據三角形的面積公式可知:SS=$\frac{1}{2}$|$\overrightarrow{{F}_{1}{F}_{2}}$||y|=$\frac{1}{2}$•2$\sqrt{3}$•|y|=$\sqrt{3}$|y|=2,代入橢圓方程,即可x2=$\frac{8}{3}$,因此$\overrightarrow{P{F}_{1}}•\overrightarrow{P{F}_{2}}$=x2+y2-3=0,即可求得$\overrightarrow{P{F}_{1}}•\overrightarrow{P{F}_{2}}$=0.
解答 解:由橢圓$\frac{{x}^{2}}{5}+\frac{{y}^{2}}{2}$=1焦點在x軸上,a=$\sqrt{5}$,b=$\sqrt{2}$,c=$\sqrt{3}$,
設P(x,y),F1(-$\sqrt{3}$,0),F2($\sqrt{3}$,0),則$\overrightarrow{P{F}_{1}}$=(-$\sqrt{3}$-x,-y),$\overrightarrow{P{F}_{2}}$=($\sqrt{3}$-x,-y),
$\overrightarrow{P{F}_{1}}•\overrightarrow{P{F}_{2}}$=(-$\sqrt{3}$-x,-y)•($\sqrt{3}$-x,-y)=x2+y2-3,
∵△F1PF2的面積S=$\frac{1}{2}$|$\overrightarrow{{F}_{1}{F}_{2}}$||y|=$\frac{1}{2}$•2$\sqrt{3}$•|y|=$\sqrt{3}$|y|=2,
∴y2=$\frac{2}{3}$,
由于點P在橢圓上,
∴$\frac{{x}^{2}}{5}+\frac{{y}^{2}}{2}$=1x,
則x2=$\frac{8}{3}$,
$\overrightarrow{P{F}_{1}}•\overrightarrow{P{F}_{2}}$=x2+y2-3=0,
故選:B.
點評 本題考查橢圓的標準方程,考查向量數量積的坐標標準,焦點三角形的面積公式,考查計算能力,屬于中檔題.


 奪冠訓練單元期末沖刺100分系列答案
奪冠訓練單元期末沖刺100分系列答案科目:高中數學 來源: 題型:解答題
 如圖,在正三棱柱ABC-A1B1C1中,點D是棱AB的中點,BC=2,AA1=2$\sqrt{3}$.
如圖,在正三棱柱ABC-A1B1C1中,點D是棱AB的中點,BC=2,AA1=2$\sqrt{3}$.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | log0.7 6<0.7 6<6 0.7 | B. | 0.7 6<6 0.7<log0.7 6 | ||
| C. | log0.7 6<6 0.7<0.76 | D. | 0.7 6<log0.7 6<6 0.7 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | [2,68] | B. | [4,68] | C. | [2,2$\sqrt{17}$] | D. | [$\sqrt{2}$,2$\sqrt{17}$] |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
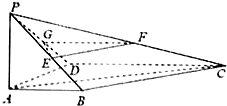 已知如圖,四邊形ABCD是直角梯形,AB∥DC,AB⊥AD,AP⊥平面ABCD,DC=2AB=2AD=2AP,點E、F、G分別是PB、PC、PD的中點.
已知如圖,四邊形ABCD是直角梯形,AB∥DC,AB⊥AD,AP⊥平面ABCD,DC=2AB=2AD=2AP,點E、F、G分別是PB、PC、PD的中點.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com