
| A. | $\frac{7}{5}$ | B. | $\frac{25}{7}$ | C. | $\frac{7}{25}$ | D. | $\frac{24}{25}$ |
分析 由條件利用同角三角函數的基本關系求得2sinαcosα的值,可得cosα-sinα=$\sqrt{{(cosα-sinα)}^{2}}$ 的值,從而求得要求式子的值.
解答 解:∵-$\frac{π}{2}$<α<0,sinα+cosα=$\frac{1}{5}$,則1+2sinαcosα=$\frac{1}{25}$,∴2sinαcosα=-$\frac{24}{25}$,
∴cosα-sinα=$\sqrt{{(cosα-sinα)}^{2}}$=$\sqrt{1+2sinαcosα}$=$\frac{7}{5}$,
則$\frac{1}{co{s}^{2}α-si{n}^{2}α}$=$\frac{1}{(cosα+sinα)•(cosα-sinα)}$=$\frac{1}{\frac{1}{5}•\frac{7}{5}}$=$\frac{25}{7}$,
故選:B.
點評 本題主要考查同角三角函數的基本關系的應用,以及三角函數在各個象限中的符號,屬于基礎題.


科目:高中數學 來源: 題型:選擇題
| A. | -$\frac{3}{2}$ | B. | -$\frac{3}{4}$ | C. | -$\frac{3}{4}$或-$\frac{3}{2}$ | D. | -1 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
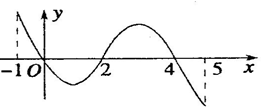 已知函數f(x)的定義域為[-1,5],部分對應值如表,f(x)的導函數y=f′(x)的圖象如圖所示,下列關于函數f(x)的命題:
已知函數f(x)的定義域為[-1,5],部分對應值如表,f(x)的導函數y=f′(x)的圖象如圖所示,下列關于函數f(x)的命題:| x | -1 | 0 | 4 | 5 |
| f(x) | 1 | 2 | 2 | 1 |
| A. | 1個 | B. | 2個 | C. | 3個 | D. | 4個 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com