
【題目】設s,t是不相等的兩個正數,且s+slnt=t+tlns,則s+t﹣st的取值范圍為( )
A.(﹣∞,1)B.(﹣∞,0)C.(0,+∞)D.(1,+∞)
科目:高中數學 來源: 題型:
【題目】在平面多邊形![]() 中,四邊形
中,四邊形![]() 是邊長為2的正方形,四邊形
是邊長為2的正方形,四邊形![]() 為等腰梯形,
為等腰梯形,![]() 為
為![]() 的中點,
的中點,![]() ,現將梯形
,現將梯形![]() 沿
沿![]() 折疊,使平面
折疊,使平面![]() 平面
平面![]() .
.
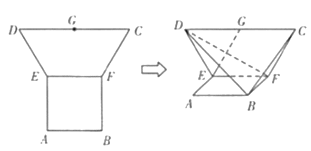
(1)求證:![]() 面
面![]() ;
;
(2)求![]() 與平面
與平面![]() 成角的正弦值.
成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠為提高生產效率,開展技術創新活動,提出了完成某項生產任務的兩種新的生產方式.為比較兩種生產方式的效率,選取![]() 名工人,將他們隨機分成兩組,每組
名工人,將他們隨機分成兩組,每組![]() 人.第一組工人用第一種生產方式,第二組工人用第二種生產方式.根據工人完成生產任務的工作時間(單位:
人.第一組工人用第一種生產方式,第二組工人用第二種生產方式.根據工人完成生產任務的工作時間(單位:![]() )繪制了如圖所示的莖葉圖(莖為十位數,葉為個位數):
)繪制了如圖所示的莖葉圖(莖為十位數,葉為個位數):
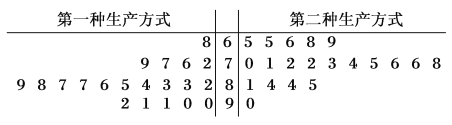
(1)根據莖葉圖,估計兩種生產方式完成任務所需時間至少![]() 分鐘的概率,并對比兩種生產方式所求概率,判斷哪種生產方式的效率更高?
分鐘的概率,并對比兩種生產方式所求概率,判斷哪種生產方式的效率更高?
(2)將完成生產任務所需時間超過![]() 和不超過
和不超過![]() 的工人數填入下面的列聯表:
的工人數填入下面的列聯表:
超過 | 不超過 | |
第一種生產方式 | ||
第二種生產方式 |
(3)根據(2)中的列聯表,能否有![]() 的把握認為兩種生產方式的效率有差異?
的把握認為兩種生產方式的效率有差異?
附: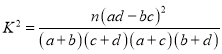
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,圓柱的軸截面ABCD是邊長為2的正方形,點P是圓弧CD上的一動點(不與C,D重合),點Q是圓弧AB的中點,且點P,Q在平面ABCD的兩側.
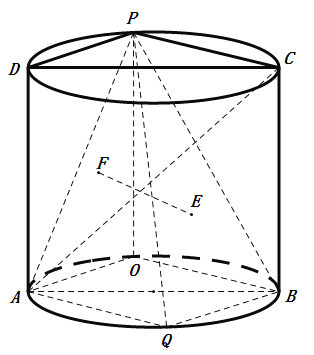
(1)證明:平面PAD⊥平面PBC;
(2)設點P在平面ABQ上的射影為點O,點E,F分別是△PQB和△POA的重心,當三棱錐P﹣ABC體積最大時,回答下列問題.
(i)證明:EF∥平面PAQ;
(ii)求平面PAB與平面PCD所成二面角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】樹立和踐行“綠水青山就是金山銀山,堅持人與自然和諧共生”的理念越來越深入人心,已形成了全民自覺參與,造福百姓的良性循環.據此,某網站推出了關于生態文明建設進展情況的調查,大量的統計數據表明,參與調查者中關注此問題的約占80%.現從參與調查的人群中隨機選出![]() 人,并將這
人,并將這![]() 人按年齡分組:第1組
人按年齡分組:第1組![]() ,第2組
,第2組![]() ,第3組
,第3組![]() ,第4組
,第4組![]() ,第5組
,第5組![]() ,得到的頻率分布直方圖如圖所示:
,得到的頻率分布直方圖如圖所示:
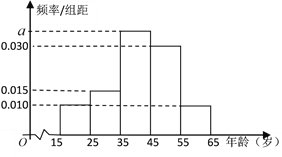
(1)求![]() 的值;
的值;
(2)求出樣本的平均數(同一組數據用該區間的中點值作代表);
(3)現在要從年齡較小的第1,2組中用分層抽樣的方法抽取![]() 人,再從這
人,再從這![]() 人中隨機抽取
人中隨機抽取![]() 人進行問卷調查,求第2組中抽到
人進行問卷調查,求第2組中抽到![]() 人的概率.
人的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com