
【題目】甲、乙兩班舉行數(shù)學知識競賽,參賽學生的競賽得分統(tǒng)計結(jié)果如下表:
班級 | 參賽人數(shù) | 平均數(shù) | 中位數(shù) | 眾數(shù) | 方差 |
甲 | 45 | 83 | 86 | 85 | 82 |
乙 | 45 | 83 | 84 | 85 | 133 |
某同學分析上表后得到如下結(jié)論:
①甲、乙兩班學生的平均成績相同;
②乙班優(yōu)秀的人數(shù)少于甲班優(yōu)秀的人數(shù)(競賽得分![]() 分為優(yōu)秀);
分為優(yōu)秀);
③甲、乙兩班成績?yōu)?/span>85分的學生人數(shù)比成績?yōu)槠渌档膶W生人數(shù)多;
④乙班成績波動比甲班小.
其中正確結(jié)論有( )
A.1個B.2個C.3個D.4個
科目:高中數(shù)學 來源: 題型:
【題目】隨著網(wǎng)絡的發(fā)展,網(wǎng)上購物越來越受到人們的喜愛,各大購物網(wǎng)站為增加收入,促銷策略越來越多樣化,促銷費用也不斷增加.下表是某購物網(wǎng)站2018年1月~8月促銷費用(萬元)和產(chǎn)品銷量(萬件)的具體數(shù)據(jù).
月份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
促銷費用 | 2 | 3 | 6 | 10 | 13 | 21 | 15 | 18 |
產(chǎn)品銷量 | 1 | 1 | 2 | 3 | 3.5 | 5 | 4 | 4.5 |
(1)根據(jù)數(shù)據(jù)可知![]() 與
與![]() 具有線性相關(guān)關(guān)系,請建立
具有線性相關(guān)關(guān)系,請建立![]() 與
與![]() 的回歸方程
的回歸方程![]() (系數(shù)精確到0.01);
(系數(shù)精確到0.01);
(2)已知6月份該購物網(wǎng)站為慶祝成立1周年,特制定獎勵制度:以![]() (單位:件)表示日銷量,
(單位:件)表示日銷量,![]() ,則每位員工每日獎勵100元;
,則每位員工每日獎勵100元;![]() ,則每位員工每日獎勵150元,
,則每位員工每日獎勵150元,![]() ,則每位員工每日獎勵200元.現(xiàn)已知該網(wǎng)站6月份日銷量
,則每位員工每日獎勵200元.現(xiàn)已知該網(wǎng)站6月份日銷量![]() 服從正態(tài)分布
服從正態(tài)分布![]() ,請你計算某位員工當月獎勵金額總數(shù)大約多少元(當月獎勵金額總數(shù)精確到百分位).
,請你計算某位員工當月獎勵金額總數(shù)大約多少元(當月獎勵金額總數(shù)精確到百分位).
參考數(shù)據(jù):![]() ,
,![]() ,其中
,其中![]() ,
,![]() 分別為第
分別為第![]() 個月的促銷費用和產(chǎn)品銷量,
個月的促銷費用和產(chǎn)品銷量,![]() .
.
參考公式:①對于一組數(shù)據(jù)![]() ,
,![]() ,…,
,…,![]() ,其回歸方程
,其回歸方程![]() 的斜率和截距的最小二乘估計分別為
的斜率和截距的最小二乘估計分別為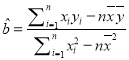 ,
,![]() ;②若隨機變量
;②若隨機變量![]() 服從正態(tài)分布
服從正態(tài)分布![]() ,則
,則![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的離心率
的離心率![]() ,且圓
,且圓![]() 過橢圓
過橢圓![]() 的上,下頂點.
的上,下頂點.
(1)求橢圓![]() 的方程.
的方程.
(2)若直線![]() 的斜率為
的斜率為![]() ,且直線
,且直線![]() 交橢圓
交橢圓![]() 于
于![]() 、
、![]() 兩點,點
兩點,點![]() 關(guān)于點的對稱點為
關(guān)于點的對稱點為![]() ,點
,點![]() 是橢圓
是橢圓![]() 上一點,判斷直線
上一點,判斷直線![]() 與
與![]() 的斜率之和是否為定值,如果是,請求出此定值:如果不是,請說明理.
的斜率之和是否為定值,如果是,請求出此定值:如果不是,請說明理.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設數(shù)列![]()
![]() 是公差不為零等差數(shù)列,滿足
是公差不為零等差數(shù)列,滿足![]() ;數(shù)列
;數(shù)列![]()
![]() 的前
的前![]() 項和為
項和為![]() ,且滿足
,且滿足![]() .
.
(1)求數(shù)列![]() 、
、![]() 的通項公式;
的通項公式;
(2)在![]() 和
和![]() 之間插入1個數(shù)
之間插入1個數(shù)![]() ,使
,使![]() 成等差數(shù)列;在
成等差數(shù)列;在![]() 和
和![]() 之間插入2個數(shù)
之間插入2個數(shù)![]() ,使
,使![]() 成等差數(shù)列;……;在
成等差數(shù)列;……;在![]() 和
和![]() 之間插入
之間插入![]() 個數(shù)
個數(shù)![]() ,使
,使![]() 成等差數(shù)列,
成等差數(shù)列,
(i)求![]() ;
;
(ii)是否存在正整數(shù)![]() ,使
,使![]() 成立?若存在,求出所有的正整數(shù)對
成立?若存在,求出所有的正整數(shù)對![]() ;若不存在,請說明理由.
;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)當![]() 時,判斷
時,判斷![]() 在定義域上的單調(diào)性;
在定義域上的單調(diào)性;
(2)若對定義域上的任意的![]() ,有
,有![]() 恒成立,求實數(shù)a的取值范圍;
恒成立,求實數(shù)a的取值范圍;
(3)證明:![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)若曲線![]() 在
在![]() 處的切線方程為
處的切線方程為![]() ,求實數(shù)
,求實數(shù)![]() ,
,![]() 的值;
的值;
(2)若![]() ,且
,且![]() 在區(qū)間
在區(qū)間![]() 上恒成立,求實數(shù)
上恒成立,求實數(shù)![]() 的取值范圍;
的取值范圍;
(3)若![]() ,且
,且![]() ,討論函數(shù)
,討論函數(shù)![]() 的單調(diào)性.
的單調(diào)性.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)當![]() 時,試討論函數(shù)
時,試討論函數(shù)![]() 的單調(diào)性,并求出函數(shù)
的單調(diào)性,并求出函數(shù)![]() 的極值;
的極值;
(2)若![]() 恒成立,求
恒成立,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某學校成立了數(shù)學、英語、音樂3個課外興趣小組,3個小組分別有39、32、33個成員,一些成員參加了不止一個小組,具體情況如圖所示.
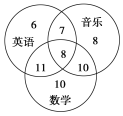
現(xiàn)隨機選取一個成員,他屬于至少2個小組的概率是________,他屬于不超過2個小組的概率是________.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com