
【題目】如圖,OA,OB是兩條互相垂直的筆直公路,半徑OA=2km的扇形AOB是某地的一名勝古跡區域.當地政府為了緩解該古跡周圍的交通壓力,欲在圓弧AB上新增一個入口P(點P不與A,B重合),并新建兩條都與圓弧AB相切的筆直公路MB,MN,切點分別是B,P.當新建的兩條公路總長最小時,投資費用最低.設∠POA=![]() ,公路MB,MN的總長為
,公路MB,MN的總長為![]() .
.

(1)求![]() 關于
關于![]() 的函數關系式,并寫出函數的定義域;
的函數關系式,并寫出函數的定義域;
(2)當![]() 為何值時,投資費用最低?并求出
為何值時,投資費用最低?并求出![]() 的最小值.
的最小值.
 考前必練系列答案
考前必練系列答案科目:高中數學 來源: 題型:
【題目】某理科考生參加自主招生面試,從7道題中(4道理科題3道文科題)不放回地依次任取3道作答.
(1)求該考生在第一次抽到理科題的條件下,第二次和第三次均抽到文科題的概率;
(2)規定理科考生需作答兩道理科題和一道文科題,該考生答對理科題的概率均為![]() ,答對文科題的概率均為
,答對文科題的概率均為![]() ,若每題答對得10分,否則得零分.現該生已抽到三道題(兩理一文),求其所得總分
,若每題答對得10分,否則得零分.現該生已抽到三道題(兩理一文),求其所得總分![]() 的分布列與數學期望
的分布列與數學期望![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=1+x﹣ ![]() +
+ ![]() ﹣
﹣ ![]() ﹣…+
﹣…+ ![]() ﹣
﹣ ![]() +
+ ![]() ,則下列結論正確的是( )
,則下列結論正確的是( )
A.f(x)在(0,1)上恰有一個零點
B.f(x)在(0,1)上恰有兩個零點
C.f(x)在(﹣1,0)上恰有一個零點
D.f(x)在(﹣1,0)上恰有兩個零點
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某中學為研究學生的身體素質與課外體育鍛煉時間的關系,對該校200名高三學生的課外體育鍛煉平均每天運動的時間進行調查,如下表:(平均每天鍛煉的時間單位:分鐘)
將學生日均課外體育運動時間在![]() 上的學生評價為“課外體育達標”.
上的學生評價為“課外體育達標”.
平均每天鍛煉的時間(分鐘) |
|
|
|
|
|
|
總人數 | 20 | 36 | 44 | 50 | 40 | 10 |
(1)請根據上述表格中的統計數據填寫下面![]() 列聯表,并通過計算判斷是否能在犯錯誤的概率不超過
列聯表,并通過計算判斷是否能在犯錯誤的概率不超過![]() 的前提下認為“課外體育達標”與性別有關?
的前提下認為“課外體育達標”與性別有關?
課外體育不達標 | 課外體育達標 | 合計 | |
男 | |||
女 | 20 | 110 | |
合計 |
(2)從上述200名學生中,按“課外體育達標”、“課外體育不達標”分層抽樣,抽取4人得到一個樣本,再從這個樣本中抽取2人,求恰好抽到一名“課外體育不達標”學生的概率.
參考公式:![]() ,其中
,其中![]() .
.
參考數據:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知m、n∈R+ , f(x)=|x+m|+|2x﹣n|.
(1)求f(x)的最小值;
(2)若f(x)的最小值為2,證明:4(m2+ ![]() )的最小值為8.
)的最小值為8.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數f(x)的定義域D={x|x≠0},且滿足對于任意x1,x2∈D.有f(x1·x2)=f(x1)+f(x2).
(1)求f(1)的值;
(2)判斷f(x)的奇偶性并證明;
(3)如果f(4)=1,f(3x+1)+f(2x-6)≤3,且f(x)在(0,+∞)上是增函數,求x的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,為一臺冷軋機的示意圖,冷軋機由若干對軋輥組成,帶鋼從一端輸入,經過各對軋輥逐步減薄后輸出.(軋鋼過程中,鋼帶寬度不變,且不考慮損耗)
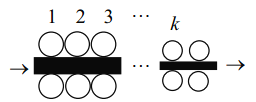
一對對軋輥的減薄率![]() .
.
(1)輸入鋼帶的厚度為![]() ,輸出鋼帶的厚度為
,輸出鋼帶的厚度為![]() ,若每對軋輥的減薄率不超過
,若每對軋輥的減薄率不超過![]() ,問冷軋機至少需要安裝幾對軋輥?
,問冷軋機至少需要安裝幾對軋輥?
(2)已知一臺冷軋機共有4對減薄率為![]() 的軋輥,所有軋輥周長均為
的軋輥,所有軋輥周長均為![]() ,若第
,若第![]() 對軋輥有缺陷,每滾動一周在剛帶上壓出一個疵點,在冷軋機輸出的剛帶上,疵點的間距為
對軋輥有缺陷,每滾動一周在剛帶上壓出一個疵點,在冷軋機輸出的剛帶上,疵點的間距為![]() ,易知
,易知![]() ,為了便于檢修,請計算
,為了便于檢修,請計算![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com