
【題目】已知橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,點
,點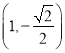 是橢圓
是橢圓![]() 上的點,離心率
上的點,離心率![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)點![]() 在橢圓
在橢圓![]() 上,若點
上,若點![]() 與點
與點![]() 關于原點對稱,連接
關于原點對稱,連接![]() 并延長與橢圓
并延長與橢圓![]() 的另一個交點為
的另一個交點為![]() ,連接
,連接![]() ,求
,求![]() 面積的最大值.
面積的最大值.
【答案】(1)![]() (2)
(2)![]()
【解析】試題分析:(1)根據條件列出關于![]() 兩個方程,解方程組可得
兩個方程,解方程組可得![]() 值,即得橢圓
值,即得橢圓![]() 的方程;(2)聯立直線方程與橢圓方程,利用韋達定理及弦長公式可得底邊長
的方程;(2)聯立直線方程與橢圓方程,利用韋達定理及弦長公式可得底邊長![]() (用直線斜率表示),根據點到直線距離公式可得三角形的高(用直線斜率表示),根據三角形面積公式可得
(用直線斜率表示),根據點到直線距離公式可得三角形的高(用直線斜率表示),根據三角形面積公式可得![]() 面積,關于直線斜率的函數關系式,最后根據分式函數求值域方法求函數最值,注意討論斜率不存在的情形.
面積,關于直線斜率的函數關系式,最后根據分式函數求值域方法求函數最值,注意討論斜率不存在的情形.
試題解析:(1)依題意,![]() ,
,![]() ,
,![]() ,解得
,解得![]() 。
。
故橢圓![]() 的方程為
的方程為![]() .
.
(2)當直線![]() 的斜率不存在時,不妨取
的斜率不存在時,不妨取![]() ,
,
故![]() .
.
②當直線![]() 的斜率存在時,設直線
的斜率存在時,設直線![]() 的方程為
的方程為![]() ,
,
聯立方程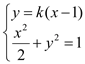 化簡得
化簡得![]() ,
,
設![]() ,則
,則![]() ,
,
![]() ,
,
點![]() 到直線
到直線![]() 的距離
的距離![]() ,
,
因為![]() 是線段
是線段![]() 的中點,所以點
的中點,所以點![]() 到直線
到直線![]() 的距離為
的距離為![]() ,
,
∴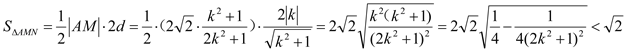 .
.
綜上,![]() 面積的最大值為
面積的最大值為![]() .
.


 怎樣學好牛津英語系列答案
怎樣學好牛津英語系列答案科目:高中數學 來源: 題型:
【題目】已知數列{an}是一個公差大于0的等差數列,且滿足![]() ,a2+a7=16
,a2+a7=16
(1)求數列{an}的通項公式;
(2)數列{an}和數列{bn}滿足等式![]() (n∈N*),求數列{bn}的前n項和Sn.
(n∈N*),求數列{bn}的前n項和Sn.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,半徑為![]() 的圓形紙板內有一個相同圓心的半徑為
的圓形紙板內有一個相同圓心的半徑為![]() 的小圓,現將半徑為
的小圓,現將半徑為![]() 的一枚硬幣拋到此紙板上,使整塊硬幣完全隨機落在紙板內,則硬幣與小圓無公共點的概率為( )
的一枚硬幣拋到此紙板上,使整塊硬幣完全隨機落在紙板內,則硬幣與小圓無公共點的概率為( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校為倡導全體學生為特困學生捐款,舉行“一元錢,一片心,誠信用水”活動,學生在購水處每領取一瓶礦泉水,便自覺向捐款箱中至少投入一元錢.現統計了連續5天的售出和收益情況,如表:
售出水量x(單位:箱) | 7 | 6 | 6 | 5 | 6 |
收益y(單位:元) | 165 | 142 | 148 | 125 | 150 |
(1)求y關于x的線性回歸方程;
(2)預測售出8箱水的收益是多少元?
附:回歸直線的斜率和截距的最小二乘法估計公式分別為: ![]() =
= 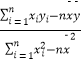 ,
, ![]() =
= ![]() ﹣
﹣ ![]()
![]() ,
,
參考數據:7×165+6×142+6×148+5×125+6×150=4420.
查看答案和解析>>
科目:高中數學 來源: 題型:
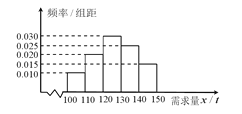
【題目】經銷商經銷某種農產品,在一個銷售季度內,每售出![]() 該產品獲利潤500元,未售出的產品,每
該產品獲利潤500元,未售出的產品,每![]() 虧損300元.根據歷史資料,得到銷售季度內市場需求量的頻率分布直圖,如圖所示.經銷商為下一個銷售季度購進了
虧損300元.根據歷史資料,得到銷售季度內市場需求量的頻率分布直圖,如圖所示.經銷商為下一個銷售季度購進了![]() 該農產品.以
該農產品.以![]() (
(![]() )表示下一個銷售季度內的市場需求量,
)表示下一個銷售季度內的市場需求量, ![]() (單位:元)表示下一個銷售季度內經銷該農產品的利潤.
(單位:元)表示下一個銷售季度內經銷該農產品的利潤.
(Ⅰ)將![]() 表示為
表示為![]() 的函數;
的函數;
(Ⅱ)根據直方圖估計利潤![]() 不少于57000元的概率.
不少于57000元的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示的空間幾何體中,底面四邊形![]() 為正方形,
為正方形, ![]() ,
, ![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
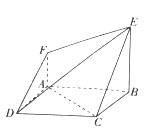
(1)求二面角![]() 的大小;
的大小;
(2)若在平面![]() 上存在點
上存在點![]() ,使得
,使得![]() 平面
平面![]() ,試通過計算說明點
,試通過計算說明點![]() 的位置.
的位置.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,已知 ![]() tanAtanB﹣tanA﹣tanB=
tanAtanB﹣tanA﹣tanB= ![]() .
.
(1)求∠C的大小;
(2)設角A,B,C的對邊依次為a,b,c,若c=2,且△ABC是銳角三角形,求a2+b2的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】【廣東省惠州市2017屆高三上學期第二次調研】已知點![]() ,點
,點![]() 是圓
是圓![]()
![]() 上的任意一點,線段
上的任意一點,線段![]() 的垂直平分線與直線
的垂直平分線與直線![]() 交于點
交于點![]() .
.
(Ⅰ)求點![]() 的軌跡方程;
的軌跡方程;
(Ⅱ)若直線![]() 與點
與點![]() 的軌跡有兩個不同的交點
的軌跡有兩個不同的交點![]() 和
和![]() ,且原點
,且原點![]() 總在以
總在以![]() 為直徑的圓的內部,求實數
為直徑的圓的內部,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱柱ABC﹣A1B1C1中,AA1⊥底面ABC,∠BAC=90°,AB=AC=2, ![]() .M,N分別為BC和CC1的中點,P為側棱BB1上的動點.
.M,N分別為BC和CC1的中點,P為側棱BB1上的動點. 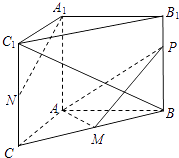
(1)求證:平面APM⊥平面BB1C1C;
(2)若P為線段BB1的中點,求證:A1N∥平面APM;
(3)試判斷直線BC1與平面APM是否能夠垂直.若能垂直,求PB的值;若不能垂直,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com