
【題目】據《人民網》報道,美國國家航空航天局(NASA)發文稱,相比20年前世界變得更綠色了,衛星資料顯示中國和印度的行動主導了地球變綠.據統計,中國新增綠化面積的![]() 來自于植樹造林,下表是中國十個地區在去年植樹造林的相關數據.(造林總面積為人工造林、飛播造林、新封山育林、退化林修復、人工更新的面積之和)
來自于植樹造林,下表是中國十個地區在去年植樹造林的相關數據.(造林總面積為人工造林、飛播造林、新封山育林、退化林修復、人工更新的面積之和)
單位:公頃
地區 | 造林總面積 | 造林方式 | ||||
人工造林 | 飛播造林 | 新封山育林 | 退化林修復 | 人工更新 | ||
內蒙 | 618484 | 311052 | 74094 | 136006 | 90382 | 6950 |
河北 | 583361 | 345625 | 33333 | 13507 | 65653 | 3643 |
河南 | 149002 | 97647 | 13429 | 22417 | 15376 | 133 |
重慶 | 226333 | 100600 | 62400 | 63333 | ||
陜西 | 297642 | 184108 | 33602 | 63865 | 16067 | |
甘肅 | 325580 | 260144 | 57438 | 7998 | ||
新疆 | 263903 | 118105 | 6264 | 126647 | 10796 | 2091 |
青海 | 178414 | 16051 | 159734 | 2629 | ||
寧夏 | 91531 | 58960 | 22938 | 8298 | 1335 | |
北京 | 19064 | 10012 | 4000 | 3999 | 1053 | |
(1)請根據上述數據分別寫出在這十個地區中人工造林面積與造林總面積的比值最大和最小的地區;
(2)在這十個地區中,任選一個地區,求該地區新封山育林面積占造林總面積的比值超過![]() 的概率;
的概率;
(3)在這十個地區中,從退化林修復面積超過一萬公頃的地區中,任選兩個地區,記X為這兩個地區中退化林修復面積超過六萬公頃的地區的個數,求X的分布列及數學期望.
【答案】(1)人工造林面積與總面積比最大的地區為甘肅省,人工造林面積與總面積比最小的地區為青海省;(2)![]() ;(3)分布列見詳解,數學期望為
;(3)分布列見詳解,數學期望為![]()
【解析】
(1)通過數據的觀察以及計算人工造林面積與造林總面積比值,可得結果.
(2)通過數據的觀察以及計算新封山育林面積與造林總面積比值,得出比值超過![]() 的地區個數,然后可得結果.
的地區個數,然后可得結果.
(3)計算退化林修復面積超過一萬公頃的地區中選兩個地區總數![]() ,退化林修復面積超過六萬公頃的地區的個數為
,退化林修復面積超過六萬公頃的地區的個數為![]() ,列出
,列出![]() 所有取值并計算相應概率,然后可得結果.
所有取值并計算相應概率,然后可得結果.
(1)人工造林面積與總面積比最大的地區為甘肅省,
人工造林面積與總面積比最小的地區為青海省.
(2)記事件A:在這十個地區中,任選一個地區,該地區
新封山育林面積占總面積的比值超過![]()
根據數據可知:青海地區人工造林面積占總面積比超過![]() ,
,
則![]()
(3)退化林修復面積超過一萬公頃有6個地區:
內蒙、河北、河南、重慶、陜西、新疆,
其中退化林修復面積超過六萬公頃有3個地區:
內蒙、河北、重慶,
所以X的取值為0,1,2
所以![]() ,
,![]() ,
,
![]()
隨機變量X的分布列如下:
|
|
|
|
|
|
|
|
![]()


科目:高中數學 來源: 題型:
【題目】設函數![]() ,過點
,過點![]() 作
作![]() 軸的垂線
軸的垂線![]() 交函數
交函數![]() 圖象于點
圖象于點![]() ,以
,以![]() 為切點作函數
為切點作函數![]() 圖象的切線交
圖象的切線交![]() 軸于點
軸于點![]() ,再過
,再過![]() 作
作![]() 軸的垂線
軸的垂線![]() 交函數
交函數![]() 圖象于點
圖象于點![]() ,
,![]() ,以此類推得點
,以此類推得點![]() ,記
,記![]() 的橫坐標為
的橫坐標為![]() ,
,![]() .
.
(1)證明數列![]() 為等比數列并求出通項公式;
為等比數列并求出通項公式;
(2)設直線![]() 與函數
與函數![]() 的圖象相交于點
的圖象相交于點![]() ,記
,記![]() (其中
(其中![]() 為坐標原點),求數列
為坐標原點),求數列![]() 的前
的前![]() 項和
項和![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解某中學學生對《中華人民共和國交通安全法》的了解情況,調查部門在該校進行了一次問卷調查(共12道題),從該校學生中隨機抽取40人,統計了每人答對的題數,將統計結果分成![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 六組,得到如下頻率分布直方圖.
六組,得到如下頻率分布直方圖.
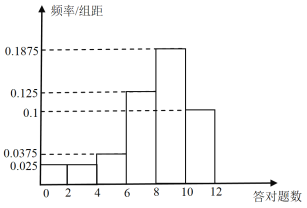
(1)若答對一題得10分,未答對不得分,估計這40人的成績的平均分(同一組中的數據用該組區間的中點值作代表);
(2)若從答對題數在![]() 內的學生中隨機抽取2人,求恰有1人答對題數在
內的學生中隨機抽取2人,求恰有1人答對題數在![]() 內的概率.
內的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某客戶考察了一款熱銷的凈水器,使用壽命為十年,過濾由核心部件濾芯來實現.在使用過程中,濾芯需要不定期更換,其中濾芯每個200元.如圖是根據100臺該款凈水器在十年使用期內更換的濾芯的件數制成的柱狀圖.(以100臺凈水器更換濾芯的頻率代替1臺凈水器更換濾芯發生的概率)
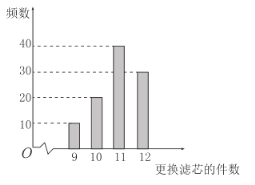
(1)估計一臺凈水器在使用期內更換濾芯的件數的眾數和中位數.
(2)估計一臺凈水器在使用期內更換濾芯的件數大于10的概率.
(3)已知上述100臺凈水器在購機的同時購買濾芯享受5折優惠(使用過程中如需再購買無優惠),假設每臺凈水器在購機的同時購買濾芯10個,這100臺凈水器在使用期內,更換濾芯的件數記為a,所需費用記為y,補全下表,估計這100臺凈水器在使用期內購買濾芯所需總費用的平均數.
100臺該款凈水器在試用期內更換濾芯的件數a | 9 | 10 | 11 | 12 |
頻數 | ||||
費用y |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義:從數列{an}中抽取m(m∈N,m≥3)項按其在{an}中的次序排列形成一個新數列{bn},則稱{bn}為{an}的子數列;若{bn}成等差(或等比),則稱{bn}為{an}的等差(或等比)子數列.
(1)記數列{an}的前n項和為Sn,已知![]() .
.
①求數列{an}的通項公式;
②數列{an}是否存在等差子數列,若存在,求出等差子數列;若不存在,請說明理由.
(2)已知數列{an}的通項公式為an=n+a(a∈Q+),證明:{an}存在等比子數列.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,橢圓
中,橢圓![]() :
:![]() 的離心率為
的離心率為![]() ,左、右頂點分別為
,左、右頂點分別為![]() 、
、![]() ,線段
,線段![]() 的長為4.點
的長為4.點![]() 在橢圓
在橢圓![]() 上且位于第一象限,過點
上且位于第一象限,過點![]() ,
,![]() 分別作
分別作![]() ,
,![]() ,直線
,直線![]() ,
,![]() 交于點
交于點![]() .
.
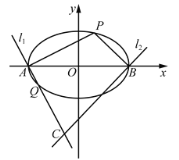
(1)若點![]() 的橫坐標為-1,求點
的橫坐標為-1,求點![]() 的坐標;
的坐標;
(2)直線![]() 與橢圓
與橢圓![]() 的另一交點為
的另一交點為![]() ,且
,且![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 是定義在R上的奇函數,當
是定義在R上的奇函數,當![]() 時,
時,![]() ,給出下列命題:
,給出下列命題:
①當![]() 時,
時,![]() ;
;
②函數![]() 有2個零點;
有2個零點;
③![]() 的解集為
的解集為![]() ;
;
④![]() ,
,![]() ,都有
,都有![]() .
.
其中真命題的個數為( )
A.4B.3C.2D.1
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左右焦點分別為
的左右焦點分別為![]() 和
和![]() ,由4個點
,由4個點![]() 、
、![]() 、
、![]() 和
和![]() 組成了一個高為
組成了一個高為![]() ,面積為
,面積為![]() 的等腰梯形.
的等腰梯形.
(1)求橢圓的方程;
(2)過點![]() 的直線和橢圓交于兩點
的直線和橢圓交于兩點![]() 、
、![]() ,求
,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com