
【題目】對于很多人來說,提前消費的認識首先是源于信用卡,在那個工資不高的年代,信用卡絕對是神器,稍微大件的東西都是可以選擇用信用卡來買,甚至于分期買,然后慢慢還!現在銀行貸款也是很風靡的,從房貸到車貸到一般的現金貸.信用卡“忽如一夜春風來”,遍布了各大小城市的大街小巷.為了解信用卡在![]() 市的使用情況,某調查機構借助網絡進行了問卷調查,并從參與調查的網友中隨機抽取了100人進行抽樣分析,得到如下
市的使用情況,某調查機構借助網絡進行了問卷調查,并從參與調查的網友中隨機抽取了100人進行抽樣分析,得到如下![]() 列聯表(單位:人)
列聯表(單位:人)
經常使用信用卡 | 偶爾或不用信用卡 | 合計 | |
40歲及以下 | 15 | 35 | 50 |
40歲以上 | 20 | 30 | 50 |
合計 | 35 | 65 | 100 |
(1)根據以上數據,能否在犯錯誤的概率不超過0.10的前提下認為![]() 市使用信用卡情況與年齡有關?
市使用信用卡情況與年齡有關?
(2)①現從所抽取的40歲及以下的網民中,按“經常使用”與“偶爾或不用”這兩種類型進行分層抽樣抽取10人,然后,再從這10人中隨機選出4人贈送積分,求選出的4人中至少有3人偶爾或不用信用卡的概率;
②將頻率視為概率,從![]() 市所有參與調查的40歲以上的網民中隨機抽取3人贈送禮品,記其中經常使用信用卡的人數為
市所有參與調查的40歲以上的網民中隨機抽取3人贈送禮品,記其中經常使用信用卡的人數為![]() ,求隨機變量
,求隨機變量![]() 的分布列、數學期望和方差.
的分布列、數學期望和方差.
參考公式: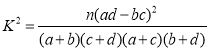 ,其中
,其中![]() .
.
參考數據:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
【答案】(1)不能在犯錯誤的概率不超過0.10的前提下認為![]() 市使用信用卡情況與年齡有關;(2)①
市使用信用卡情況與年齡有關;(2)①![]() ;②分布列見解析,
;②分布列見解析,![]() ,
,![]()
【解析】
(1)計算![]() 再對照表格分析即可.
再對照表格分析即可.
(2)①根據分層抽樣的方法可得經常使用信用卡的有![]() 人,偶爾或不用信用卡的有
人,偶爾或不用信用卡的有![]() 人,再根據超幾何分布的方法計算3人或4人偶爾或不用信用卡的概率即可.
人,再根據超幾何分布的方法計算3人或4人偶爾或不用信用卡的概率即可.
②利用二項分布的特點求解變量![]() 的分布列、數學期望和方差即可.
的分布列、數學期望和方差即可.
(1)由列聯表可知,![]() ,因為
,因為![]() ,
,
所以不能在犯錯誤的概率不超過0.10的前提下認為![]() 市使用信用卡情況與年齡有關.
市使用信用卡情況與年齡有關.
(2)①依題意,可知所抽取的10名40歲及以下網民中,經常使用信用卡的有![]() (人),偶爾或不用信用卡的有
(人),偶爾或不用信用卡的有![]() (人).
(人).
則選出的4人中至少有3人偶爾或不用信用卡的概率![]() .
.
②由![]() 列聯表,可知40歲以上的網民中,抽到經常使用信用卡的頻率為
列聯表,可知40歲以上的網民中,抽到經常使用信用卡的頻率為![]() ,
,
將頻率視為概率,即從![]() 市市民中任意抽取1人,恰好抽到經常使用信用卡的市民的概率為
市市民中任意抽取1人,恰好抽到經常使用信用卡的市民的概率為![]() .
.
由題意得![]() ,
,
則![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
故隨機變量![]() 的分布列為:
的分布列為:
| 0 | 1 | 2 | 3 |
|
|
|
|
|
故隨機變量![]() 的數學期望為
的數學期望為![]() ,方差為
,方差為![]() .
.


 全優考典單元檢測卷及歸類總復習系列答案
全優考典單元檢測卷及歸類總復習系列答案科目:高中數學 來源: 題型:
【題目】已知等差數列{an},等比數列{bn}滿足:a1=b1=1,a2=b2,2a3-b3=1.
(1)求數列{an},{bn}的通項公式;
(2)記cn=anbn,求數列{cn}的前n項和Sn.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司訂購了一批樹苗,為了檢測這批樹苗是否合格,從中隨機抽測![]() 株樹苗的高度,經數據處理得到如圖1所示的頻率分布直方圖,其中最高的
株樹苗的高度,經數據處理得到如圖1所示的頻率分布直方圖,其中最高的![]() 株樹苗的高度的莖葉圖如圖2所示,以這
株樹苗的高度的莖葉圖如圖2所示,以這![]() 株樹苗的高度的頻率估計整批樹苗高度的概率.
株樹苗的高度的頻率估計整批樹苗高度的概率.
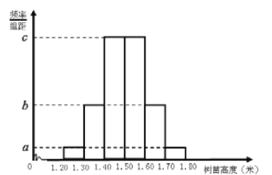

(1)求這批樹苗的高度于![]() 米的概率,并求圖
米的概率,并求圖![]() 中
中![]() 的值;
的值;
(2)若從這批樹苗中隨機選取![]() 株,記
株,記![]() 為高度在
為高度在![]() 的樹苗數量,求
的樹苗數量,求![]() 的分布列和數學期望;
的分布列和數學期望;
(3)若變量![]() 滿足
滿足![]() 且
且![]() ,則稱變量
,則稱變量![]() 滿足近似于正態分布
滿足近似于正態分布![]() 的概率分布,如果這批樹苗的高度近似于正態分布
的概率分布,如果這批樹苗的高度近似于正態分布![]() 的概率分布,則認為這批樹苗是合格的,將順利被簽收,否則,公司將拒絕簽收.試問:該批樹苗是否被簽收?
的概率分布,則認為這批樹苗是合格的,將順利被簽收,否則,公司將拒絕簽收.試問:該批樹苗是否被簽收?
查看答案和解析>>
科目:高中數學 來源: 題型:
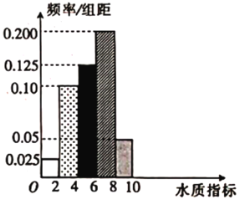
【題目】新《水污染防治法》已由中華人民共和國第十二屆全國人民代表大會常務委員會第二十八次會議于2017年6月27日通過,自2018年1月1日起施行.2018年3月1日,某縣某質檢部門隨機抽取了縣域內100眼水井,檢測其水質總體指標.
羅斯水質指數 | 02 | 24 | 46 | 68 | 810 |
水質狀況 | 腐敗污水 | 嚴重污染 | 污染 | 輕度污染 | 純凈 |
(1)求所抽取的100眼水井水質總體指標值的樣本平均數![]() (同一組中的數據用該組區間的中點值作代表).
(同一組中的數據用該組區間的中點值作代表).
(2)①由直方圖可以認為,100眼水井水質總體指標值![]() 服從正態分布
服從正態分布![]() ,利用該正態分布,求
,利用該正態分布,求![]() 落在(5.21,5.99)內的概率;
落在(5.21,5.99)內的概率;
②將頻率視為概率,若某鄉鎮抽查5眼水井的水質,記這5眼水井水質總體指標值位于(6,10)內的井數為![]() ,求
,求![]() 的分布列和數學期望.
的分布列和數學期望.
附:①計算得所抽查的這100眼水井總體指標的標準差為![]() ;
;
②若![]() ,則
,則![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年7月1日到3日,世界新能源汽車大會在海南博鰲召開,大會著眼于全球汽車產業的轉型升級和生態環境的持續改善.某汽車公司順應時代潮流,最新研發了一款新能源汽車,并在出廠前對100輛汽車進行了單次最大續航里程(理論上是指新能源汽車所裝載的燃料或電池所能夠提供給車行駛的最遠里程)的測試.現對測試數據進行分析,得到如圖的頻率分布直方圖.

(1)估計這100輛汽車的單次最大續航里程的平均值![]() (同一組中的數據用該組區間的中點值代表);
(同一組中的數據用該組區間的中點值代表);
(2)根據大量的汽車測試數據,可以認為這款汽車的單次最大續航量程X近似地服從正態分布![]() ,經計算第(1)問中樣本標準差s的近似值為50.用樣本平均數
,經計算第(1)問中樣本標準差s的近似值為50.用樣本平均數![]() 作為
作為![]() 的近似值,用樣本標準差s作為
的近似值,用樣本標準差s作為![]() 的估計值,現任取一輛汽車,求它的單次最大續航里程恰在250千米到400千米之間的概率;
的估計值,現任取一輛汽車,求它的單次最大續航里程恰在250千米到400千米之間的概率;
(3)某汽車銷售公司為推廣此款新能源汽車,現面向意向客戶推出“玩游戲,送大獎”活動,客戶可根據拋擲硬幣的結果,操控微型遙控車在方格圖上行進,若遙控車最終停在“勝利大本營”,則可獲得購車優惠券.已知硬幣出現正,反面的概率都是![]() ,方格圖上標有第0格、第1格、第2格……第50格.遙控車開始在第0格,客戶每擲一次硬幣,遙控車向前移動一次,若擲出正面,遙控車向前移動一格(從k到
,方格圖上標有第0格、第1格、第2格……第50格.遙控車開始在第0格,客戶每擲一次硬幣,遙控車向前移動一次,若擲出正面,遙控車向前移動一格(從k到![]() ),若擲出反面,遙控車向前移動兩格(從k到
),若擲出反面,遙控車向前移動兩格(從k到![]() ),直到遙控車移到第49格(勝利大本營)或第50格(失敗大本營)時,游戲結束.設遙控車移到第n格的概率為
),直到遙控車移到第49格(勝利大本營)或第50格(失敗大本營)時,游戲結束.設遙控車移到第n格的概率為![]() ,試證明
,試證明![]() 是等比數列,并解釋此方案能否成功吸引顧客購買該款新能源汽車.
是等比數列,并解釋此方案能否成功吸引顧客購買該款新能源汽車.
參考數據:若隨機變量![]() 服從正態分布
服從正態分布![]() ,則
,則![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近年來,隨著“一帶一路”倡議的推進,中國與沿線國家旅游合作越來越密切,中國到“一帶一路”沿線國家的游客人也越來越多,如圖是2013-2018年中國到“一帶一路”沿線國家的游客人次情況,則下列說法正確的是( )
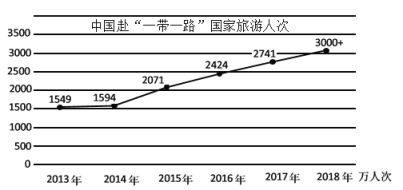
①2013-2018年中國到“一帶一路”沿線國家的游客人次逐年增加
②2013-2018年這6年中,2014年中國到“一帶一路”沿線國家的游客人次增幅最小
③2016-2018年這3年中,中國到“一帶一路”沿線國家的游客人次每年的增幅基本持平
A.①②③B.②③C.①②D.③
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com