
【題目】新《水污染防治法》已由中華人民共和國第十二屆全國人民代表大會常務委員會第二十八次會議于2017年6月27日通過,自2018年1月1日起施行.2018年3月1日,某縣某質檢部門隨機抽取了縣域內100眼水井,檢測其水質總體指標.
羅斯水質指數 | 02 | 24 | 46 | 68 | 810 |
水質狀況 | 腐敗污水 | 嚴重污染 | 污染 | 輕度污染 | 純凈 |
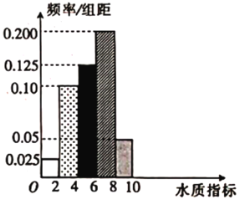
(1)求所抽取的100眼水井水質總體指標值的樣本平均數![]() (同一組中的數據用該組區間的中點值作代表).
(同一組中的數據用該組區間的中點值作代表).
(2)①由直方圖可以認為,100眼水井水質總體指標值![]() 服從正態分布
服從正態分布![]() ,利用該正態分布,求
,利用該正態分布,求![]() 落在(5.21,5.99)內的概率;
落在(5.21,5.99)內的概率;
②將頻率視為概率,若某鄉鎮抽查5眼水井的水質,記這5眼水井水質總體指標值位于(6,10)內的井數為![]() ,求
,求![]() 的分布列和數學期望.
的分布列和數學期望.
附:①計算得所抽查的這100眼水井總體指標的標準差為![]() ;
;
②若![]() ,則
,則![]() ,
,![]() .
.
 通城學典默寫能手系列答案
通城學典默寫能手系列答案科目:高中數學 來源: 題型:
【題目】在銳角△ABC中,a=2![]() ,_______,求△ABC的周長l的范圍.
,_______,求△ABC的周長l的范圍.
在①![]() (﹣cos
(﹣cos![]() ,sin
,sin![]() ),
),![]() (cos
(cos![]() ,sin
,sin![]() ),且
),且![]()
![]() ,②cosA(2b﹣c)=acosC,③f(x)=cosxcos(x
,②cosA(2b﹣c)=acosC,③f(x)=cosxcos(x![]() )
)![]() ,f(A)
,f(A)![]()
注:這三個條件中任選一個,補充在上面問題中并對其進行求解.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于很多人來說,提前消費的認識首先是源于信用卡,在那個工資不高的年代,信用卡絕對是神器,稍微大件的東西都是可以選擇用信用卡來買,甚至于分期買,然后慢慢還!現在銀行貸款也是很風靡的,從房貸到車貸到一般的現金貸.信用卡“忽如一夜春風來”,遍布了各大小城市的大街小巷.為了解信用卡在![]() 市的使用情況,某調查機構借助網絡進行了問卷調查,并從參與調查的網友中隨機抽取了100人進行抽樣分析,得到如下
市的使用情況,某調查機構借助網絡進行了問卷調查,并從參與調查的網友中隨機抽取了100人進行抽樣分析,得到如下![]() 列聯表(單位:人)
列聯表(單位:人)
經常使用信用卡 | 偶爾或不用信用卡 | 合計 | |
40歲及以下 | 15 | 35 | 50 |
40歲以上 | 20 | 30 | 50 |
合計 | 35 | 65 | 100 |
(1)根據以上數據,能否在犯錯誤的概率不超過0.10的前提下認為![]() 市使用信用卡情況與年齡有關?
市使用信用卡情況與年齡有關?
(2)①現從所抽取的40歲及以下的網民中,按“經常使用”與“偶爾或不用”這兩種類型進行分層抽樣抽取10人,然后,再從這10人中隨機選出4人贈送積分,求選出的4人中至少有3人偶爾或不用信用卡的概率;
②將頻率視為概率,從![]() 市所有參與調查的40歲以上的網民中隨機抽取3人贈送禮品,記其中經常使用信用卡的人數為
市所有參與調查的40歲以上的網民中隨機抽取3人贈送禮品,記其中經常使用信用卡的人數為![]() ,求隨機變量
,求隨機變量![]() 的分布列、數學期望和方差.
的分布列、數學期望和方差.
參考公式: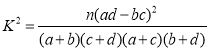 ,其中
,其中![]() .
.
參考數據:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某蛋糕店計劃按天生產一種面包,每天生產量相同,生產成本每個6元,售價每個8元,未售出的面包降價處理,以每個5元的價格當天全部處理完.
(1)若該蛋糕店一天生產30個這種面包,求當天的利潤y(單位:元)關于當天需求量n(單位:個,![]() )的函數解析式;
)的函數解析式;
(2)蛋糕店記錄了30天這種面包的日需求量(單位:個),整理得表:
日需求量n | 28 | 29 | 30 | 31 | 32 | 33 |
頻數 | 3 | 4 | 6 | 6 | 7 | 4 |
假設蛋糕店在這30天內每天生產30個這種面包,求這30天的日利潤(單位:元)的平均數及方差;
(3)蛋糕店規定:若連續10天的日需求量都不超過10個,則立即停止這種面包的生產,現給出連續10天日需求量的統計數據為“平均數為6,方差為2”,試根據該統計數據決策是否一定要停止這種面包的生產?并給出理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() 是兩個非零平面向量,則有:
是兩個非零平面向量,則有:
①若![]() ,則
,則![]()
②若![]() ,則
,則![]()
③若![]() ,則存在實數
,則存在實數![]() ,使得
,使得![]()
④若存在實數![]() ,使得
,使得![]() ,則
,則![]() 或
或![]() 四個命題中真命題的序號為 __________.(填寫所有真命題的序號)
四個命題中真命題的序號為 __________.(填寫所有真命題的序號)
【答案】①③④
【解析】逐一考查所給的結論:
①若![]() ,則
,則![]() ,據此有:
,據此有:![]() ,說法①正確;
,說法①正確;
②若![]() ,取
,取![]() ,則
,則![]() ,
,
而![]() ,說法②錯誤;
,說法②錯誤;
③若![]() ,則
,則![]() ,據此有:
,據此有:![]() ,
,
由平面向量數量積的定義有:![]() ,
,
則向量![]() 反向,故存在實數
反向,故存在實數![]() ,使得
,使得![]() ,說法③正確;
,說法③正確;
④若存在實數![]() ,使得
,使得![]() ,則向量
,則向量![]() 與向量
與向量![]() 共線,
共線,
此時![]() ,
,![]() ,
,
若題中所給的命題正確,則![]() ,
,
該結論明顯成立.即說法④正確;
綜上可得:真命題的序號為①③④.
點睛:處理兩個向量的數量積有三種方法:利用定義;利用向量的坐標運算;利用數量積的幾何意義.具體應用時可根據已知條件的特征來選擇,同時要注意數量積運算律的應用.
【題型】填空題
【結束】
17
【題目】已知在![]() 中,
中,![]() ,且
,且![]() .
.
(1)求角![]() 的大小;
的大小;
(2)設數列![]() 滿足
滿足![]() ,前
,前![]() 項和為
項和為![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】依據某地某條河流8月份的水文觀測點的歷史統計數據所繪制的頻率分布直方圖如圖(甲)所示;依據當地的地質構造,得到水位與災害等級的頻率分布條形圖如圖(乙)所示.
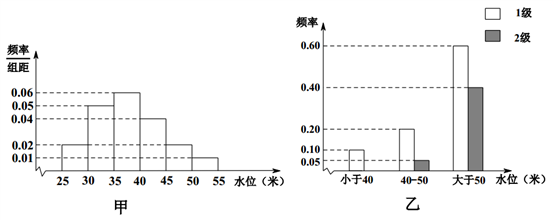
試估計該河流在8月份水位的中位數;
(1)以此頻率作為概率,試估計該河流在8月份發生1級災害的概率;
(2)該河流域某企業,在8月份,若沒受1、2級災害影響,利潤為500萬元;若受1級災害影響,則虧損100萬元;若受2級災害影響則虧損1000萬元.
現此企業有如下三種應對方案:
方案 | 防控等級 | 費用(單位:萬元) |
方案一 | 無措施 | 0 |
方案二 | 防控1級災害 | 40 |
方案三 | 防控2級災害 | 100 |
試問,如僅從利潤考慮,該企業應選擇這三種方案中的哪種方案?說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】北京地鐵八通線西起四惠站,東至土橋站,全長18.964km,共設13座車站.目前八通線執行2014年12月28日制訂的計價標準,各站間計程票價(單位:元)如下:
四惠 | 3 | 3 | 3 | 3 | 4 | 4 | 4 | 5 | 5 | 5 | 5 | 5 | |
四惠東 | 3 | 3 | 3 | 4 | 4 | 4 | 5 | 5 | 5 | 5 | 5 | ||
高碑店 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 5 | 5 | p>5 | |||
傳媒大學 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 5 | 5 | ||||
雙橋 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 4 | |||||
管莊 | 3 | 3 | 3 | 3 | 4 | 4 | 4 | ||||||
八里橋 | 3 | 3 | 3 | 3 | 4 | 4 | |||||||
通州北苑 | 3 | 3 | 3 | 3 | 3 | ||||||||
果園 | 3 | 3 | 3 | 3 | |||||||||
九棵樹 | 3 | 3 | 3 | ||||||||||
梨園 | /p> | 3 | 3 | ||||||||||
臨河里 | 3 | ||||||||||||
土橋 | |||||||||||||
四惠 | 四惠東 | 高碑店 | 傳媒大學 | 雙橋 | 管莊 | 八里橋 | 通州北苑 | 果園 | 九棵樹 | 梨園 | 臨河里 | 土橋 |
(Ⅰ)在13座車站中任選兩個不同的車站,求兩站間票價不足5元的概率;
(Ⅱ)甲乙二人從四惠站上車乘坐八通線,各自任選另一站下車(二人可同站下車),記甲乙二人乘車購票花費之和為X元,求X的分布列;
(Ⅲ)若甲乙二人只乘坐八通線,甲從四惠站上車,任選另一站下車,記票價為![]() 元;乙從土橋站上車,任選另一站下車,記票價為
元;乙從土橋站上車,任選另一站下車,記票價為![]() 元.試比較
元.試比較![]() 和
和![]() 的方差
的方差![]() 和
和![]() 大小.(結論不需要證明)
大小.(結論不需要證明)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() 、
、![]() 是空間兩條不同的直線,
是空間兩條不同的直線,![]() 、
、![]() 是空間兩個不同的平面.給出下列四個命題:
是空間兩個不同的平面.給出下列四個命題:
①若![]() ,
,![]() ,
,![]() ,則
,則![]() ;
;
②若![]() ,
,![]() ,
,![]() ,則
,則![]() ;
;
③若![]() ,
,![]() ,
,![]() ,則
,則![]() ;
;
④若![]() ,
,![]() ,
,![]() ,
,![]() ,則
,則![]() .
.
其中正確的是__________(填序號).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com