
【題目】設![]() 、
、![]() 是空間兩條不同的直線,
是空間兩條不同的直線,![]() 、
、![]() 是空間兩個不同的平面.給出下列四個命題:
是空間兩個不同的平面.給出下列四個命題:
①若![]() ,
,![]() ,
,![]() ,則
,則![]() ;
;
②若![]() ,
,![]() ,
,![]() ,則
,則![]() ;
;
③若![]() ,
,![]() ,
,![]() ,則
,則![]() ;
;
④若![]() ,
,![]() ,
,![]() ,
,![]() ,則
,則![]() .
.
其中正確的是__________(填序號).
科目:高中數學 來源: 題型:
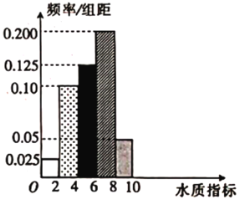
【題目】新《水污染防治法》已由中華人民共和國第十二屆全國人民代表大會常務委員會第二十八次會議于2017年6月27日通過,自2018年1月1日起施行.2018年3月1日,某縣某質檢部門隨機抽取了縣域內100眼水井,檢測其水質總體指標.
羅斯水質指數 | 02 | 24 | 46 | 68 | 810 |
水質狀況 | 腐敗污水 | 嚴重污染 | 污染 | 輕度污染 | 純凈 |
(1)求所抽取的100眼水井水質總體指標值的樣本平均數![]() (同一組中的數據用該組區間的中點值作代表).
(同一組中的數據用該組區間的中點值作代表).
(2)①由直方圖可以認為,100眼水井水質總體指標值![]() 服從正態分布
服從正態分布![]() ,利用該正態分布,求
,利用該正態分布,求![]() 落在(5.21,5.99)內的概率;
落在(5.21,5.99)內的概率;
②將頻率視為概率,若某鄉鎮抽查5眼水井的水質,記這5眼水井水質總體指標值位于(6,10)內的井數為![]() ,求
,求![]() 的分布列和數學期望.
的分布列和數學期望.
附:①計算得所抽查的這100眼水井總體指標的標準差為![]() ;
;
②若![]() ,則
,則![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某大型公司為了切實保障員工的健康安全,貫徹好衛生防疫工作的相關要求,決定在全公司范圍內舉行一次乙肝普查.為此需要抽驗669人的血樣進行化驗,由于人數較多,檢疫部門制定了下列兩種可供選擇的方案.
方案一:將每個人的血分別化驗,這時需要驗669次.
方案二:按![]() 個人一組進行隨機分組,把從每組
個人一組進行隨機分組,把從每組![]() 個人抽來的血混合在一起進行檢驗,如果每個人的血均為陰性,則驗出的結果呈陰性,這
個人抽來的血混合在一起進行檢驗,如果每個人的血均為陰性,則驗出的結果呈陰性,這![]() 個人的血就只需檢驗一次(這時認為每個人的血化驗
個人的血就只需檢驗一次(這時認為每個人的血化驗![]() 次);否則,若呈陽性,則需對這
次);否則,若呈陽性,則需對這![]() 個人的血樣再分別進行一次化驗,這時該組
個人的血樣再分別進行一次化驗,這時該組![]() 個人的血總共需要化驗
個人的血總共需要化驗![]() 次.
次.
假設此次普查中每個人的血樣化驗呈陽性的概率為![]() ,且這些人之間的試驗反應相互獨立.
,且這些人之間的試驗反應相互獨立.
(1)設方案二中,某組![]() 個人中每個人的血化驗次數為
個人中每個人的血化驗次數為![]() ,求
,求![]() 的分布列.
的分布列.
(2)設![]() ,試比較方案二中,
,試比較方案二中,![]() 分別取2,3,4時,各需化驗的平均總次數;并指出在這三種分組情況下,相比方案一,化驗次數最多可以平均減少多少次?(最后結果四舍五入保留整數)
分別取2,3,4時,各需化驗的平均總次數;并指出在這三種分組情況下,相比方案一,化驗次數最多可以平均減少多少次?(最后結果四舍五入保留整數)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近年來,隨著“一帶一路”倡議的推進,中國與沿線國家旅游合作越來越密切,中國到“一帶一路”沿線國家的游客人也越來越多,如圖是2013-2018年中國到“一帶一路”沿線國家的游客人次情況,則下列說法正確的是( )
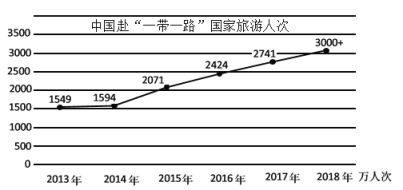
①2013-2018年中國到“一帶一路”沿線國家的游客人次逐年增加
②2013-2018年這6年中,2014年中國到“一帶一路”沿線國家的游客人次增幅最小
③2016-2018年這3年中,中國到“一帶一路”沿線國家的游客人次每年的增幅基本持平
A.①②③B.②③C.①②D.③
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】國家規定每年的![]() 月
月![]() 日以后的
日以后的![]() 天為當年的暑假.某鋼琴培訓機構對
天為當年的暑假.某鋼琴培訓機構對![]() 位鋼琴老師暑假一天的授課量進行了統計,如下表所示:
位鋼琴老師暑假一天的授課量進行了統計,如下表所示:
授課量(單位:小時) |
|
|
|
|
|
頻數 |
|
|
|
|
|
培訓機構專業人員統計近![]() 年該校每年暑假
年該校每年暑假![]() 天的課時量情況如下表:
天的課時量情況如下表:
課時量(單位:天) |
|
|
|
|
|
頻數 |
|
|
|
|
|
(同組數據以這組數據的中間值作代表)
(1)估計![]() 位鋼琴老師一日的授課量的平均數;
位鋼琴老師一日的授課量的平均數;
(2)若以(1)中確定的平均數作為上述一天的授課量.已知當地授課價為![]() 元/小時,每天的各類生活成本為
元/小時,每天的各類生活成本為![]() 元/天;若不授課,不計成本,請依據往年的統計數據,估計一位鋼琴老師
元/天;若不授課,不計成本,請依據往年的統計數據,估計一位鋼琴老師![]() 天暑假授課利潤不少于
天暑假授課利潤不少于![]() 萬元的概率.
萬元的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,以
中,以![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標系,已知曲線
軸的正半軸為極軸建立極坐標系,已知曲線![]() ,直線的參數方程為
,直線的參數方程為![]() ,(
,(![]() 為參數).直線
為參數).直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點.
兩點.
(1)寫出曲線![]() 的直角坐標方程和直線
的直角坐標方程和直線![]() 的普通方程.
的普通方程.
(2)設![]() ,若
,若![]() 成等比數列,求
成等比數列,求![]() 和的
和的![]() 值.
值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市教育局為了監控某校高一年級的素質教育過程,從該校高一年級16個班隨機抽取了16個樣本成績,制表如下:
抽取次序 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
測評成績 | 95 | 96 | 96 | 90 | 95 | 98 | 98 | 97 |
抽取次序 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
測評成績 | 97 | 95 | 96 | 98 | 99 | 96 | 99 | 96 |
令![]() 為抽取的第
為抽取的第![]() 個學生的素質教育測評成績,
個學生的素質教育測評成績,![]() ,經計算得,
,經計算得,![]() ,
,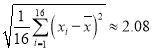 .以下計算精確到0.01.
.以下計算精確到0.01.
(1)設![]() 為抽取的16個樣本的成績,用頻率估計概率,求
為抽取的16個樣本的成績,用頻率估計概率,求![]() 的分布列、數學期望
的分布列、數學期望![]() 和標準方差
和標準方差![]() ;
;
(2)在抽取的樣本成績中,如果出現了在![]() 之外的成績,就認為本學期的素質教育過程可能出現了異常情況,需對本學期的素質教學過程進行反思,同時對下學期的素質教育過程提出指導性的建議.從該校抽樣的結果來看,是否需對本學期的素質教學過程進行反思,同時對下學期的素質教育過程提出指導性的建議?
之外的成績,就認為本學期的素質教育過程可能出現了異常情況,需對本學期的素質教學過程進行反思,同時對下學期的素質教育過程提出指導性的建議.從該校抽樣的結果來看,是否需對本學期的素質教學過程進行反思,同時對下學期的素質教育過程提出指導性的建議?
(3)列出不小于![]() 的所有樣本成績,設列出的這些成績的中位數為
的所有樣本成績,設列出的這些成績的中位數為![]() ,每次從列出的這些成績中隨機抽取1個成績,有放回地連續抽取3次,求恰好有2次抽得的成績為
,每次從列出的這些成績中隨機抽取1個成績,有放回地連續抽取3次,求恰好有2次抽得的成績為![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
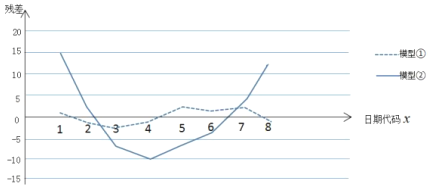
【題目】新型冠狀病毒肺炎COVID-19疫情發生以來,在世界各地逐漸蔓延.在全國人民的共同努力和各級部門的嚴格管控下,我國的疫情已經得到了很好的控制.然而,小王同學發現,每個國家在疫情發生的初期,由于認識不足和措施不到位,感染人數都會出現快速的增長.下表是小王同學記錄的某國連續8天每日新型冠狀病毒感染確診的累計人數.
日期代碼x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
累計確診人數y | 4 | 8 | 16 | 31 | 51 | 71 | 97 | 122 |
為了分析該國累計感染人數的變化趨勢,小王同學打算從①![]() ,②
,②![]() 中選擇一種模型對變量x和y的關系進行擬合,得到相應的回歸方程,經過計算得
中選擇一種模型對變量x和y的關系進行擬合,得到相應的回歸方程,經過計算得![]() ,
,![]() ,
,![]() ,
,![]() ,其中
,其中![]() ,
,![]() .
.
(1)請根據散點圖,比較模型①,②的擬合效果,小王應該選擇哪個模型?
(2)根據(1)問選定的模型求出相應的回歸方程(系數均保留一位小數);
(3)由于時差,該國截止第9天新型冠狀病毒感染確診的累計人數尚未公布.小王同學認為,如果防疫形勢沒有得到明顯改善,在數據公布之前可以根據他在(2)問求出的回歸方程來對感染人數作出預測,那么估計該地區第9天新型冠狀病毒感染確診的累計人數是多少.
附:回歸直線的最小二乘估計參考公式為: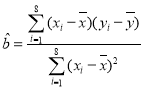 ,
,
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com